Фильтры вообще и активные фильтры, в частности, являются настолько важными устройствами электроники, что вопросам их строгого, математического описания уделялось и уделяется самое серьезное внимание.
Фильтры вообще и активные фильтры, в частности, являются настолько важными устройствами электроники, что вопросам их строгого, математического описания уделялось и уделяется самое серьезное внимание.
Публикуется большое число научных статей и книг, посвященных фильтрам. Для того чтобы инженер или научный работник был в состоянии воспользоваться указанными источниками информации, а также средствами автоматизированного проектирования, он должен хотя бы в общих чертах знать особенности математического описания фильтров.

В соответствии с изложенным фильтр описывается обыкновенным линейным дифференциальным уравнением некоторого порядка n an( dny/dtn ) + an-1( dn-1y/dtn-1 ) + … + a1( dy/dt ) + a0 y = = bm( dmx/dtm ) + bm-1( dm-1x/dtm-1 ) + …+b1(dx/dt) +b0x
где х = x(t) — входной сигнал фильтра (обычно — входное напряжение);
y = y(t) — выходной сигнал фильтра (обычно — выходное напряжение);
аi,i= 0, …, n; bi, i = 0, …, m — вещественные коэффициенты.
Для фильтров, которые могут быть реализованы, выполняется соотношение n>m. Величину n называют также порядком фильтра. Если, например, n = 2, то говорят, что фильтр второго порядка.
Необходимо отметить, что вместо записанного одного уравнения фильтр может быть описан линейной системой из n дифференциальных уравнений первого порядка (системой дифференциальных уравнений в форме Коши). Показано, что величина и равна или меньше количества реактивных элементов (конденсаторов и катушек индуктивности) фильтра.

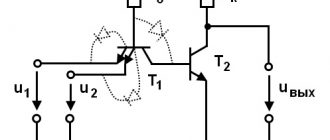
Для примера обратимся к схеме, приведенной на рис. 2.48. 
Уже до составления одного дифференциального уравнения или эквивалентной системы дифференциальных уравнений можно сказать, что это схема второго порядка, так как начальные напряжения при расчете переходного процесса можно задавать независимо для двух из трех конденсаторов.
Применим к приведенному выше уравнению прямое преобразование Лапласа и определим передаточную функцию T(s) как отношение операторного изображения Y(s) выходной величины к операторному изображению X(s) входной величины:
Т (s) = Y(s) / X(s) = = ( bmsm + bm-1sm-1 + … + b1s + b0 ) / ( ansn + an-1sn-1 + … + a1s + a0 ) где s — комплексная частота.
Запишем передаточную функцию в следующем виде: Т (s) = K · [ ( s − z1 )( s – z2 ) … ( s – zm) ] / [ ( s − p1 )( s – p2 ) …(s–pn) ] где К— вещественный коэффициент; z1 … zm — корни полинома числителя (их принято называть нулями);
p1 … pn — корни полинома знаменателя (их принято называть полюсами).
Известно, что полюсы и нули могут быть или вещественными, или комплексно-сопряженными.
Как уже отмечалось, при описании свойств фильтров обычно ориентируются на синусоидальные сигналы. При этом имеют в виду установившийся режим работы. В такой ситуации широко используют частотную передаточную функцию T(jω), которую получают из обычной передаточной функции при использовании подстановки s = jω
где ω — круговая частота, рад/сек.
Получаем T(jω) = K · [ ( jω− z1 )( jω– z2 ) … ( jω– zm) ] :: [ ( jω− p1 )( jω– p2 ) …(jω –pn) ]
Укажем три характеристики, которые широко используются для описания фильтров:
- амплитудно-частотная;
- фазочастотная;
- времени замедления (группового времени замедления).
Амплитудно-частотная характеристика
Амплитудно-частотная характеристика представляет собой зависимость вида А(ω) = | T(jω) |
Значение А(ω) на некоторой частоте дает отношение действующих (и амплитудных) значений сигналов на выходе и входе фильтра. На практике широко используют амплитудно-частотную характеристику в децибелах, которая представляет собой зависимость вида
АдБ(ω) = 20 lg|T(jω) |
Фазочастотная характеристика
Фазочастотная характеристика — это зависимость вида φ (ω) = arg T (jω)
Значение φ (ω) на некоторой частоте является сдвигом по фазе выходной величины по отношению к входной.
Характеристика времени замедления — это зависимость вида τ(ω) = −dφ(ω) /dω
Величина τ (ω) − это время замедления (групповое). Оно характеризует сдвиг по времени выходной величины по отношению к входной.
Наиболее широко используют амплитудно-частотную и фазочастотную характеристики.
Характеристика времени замедления не несет принципиально новой информации по сравнению с фазочастотной характеристикой, но является весьма полезной и используется достаточно часто. Для уяснения роли времени замедления при анализе фильтров кратко рассмотрим проблему искажения формы сигнала, содержащего несколько гармоник, при прохождении его через фильтр.

Вначале рассмотрим фильтр с настолько совершенной фазочастотной характеристикой, что искажение формы сигнала отсутствует. Такая фазочастотная характеристика является линейной однородной функцией круговой частоты и определяется выражением
φ(ω) = −kω
где k — постоянная положительная величина. Приведем соответствующий график (рис. 2.49). 
Пусть входным сигналом является напряжение u вх, содержащее две гармоники (рис. 2.50). 
Для первой гармоники фильтр обеспечивает сдвиг по фазе φ1(ω) = −kω1
Для второй гармоники сдвиг по фазе будет равен φ2(ω) = −kω2= − 2kω1

Составим пропорцию −2π / φ1 = Т1 / t1 отсюда t1 = φ1·Т1/ −2π=φ1· (1/f1) / −2π=φ1/ −ω1= − kω1/ −ω1= k
Аналогично получаем t1= φ2 / − ω2 = − 2kω1 / − 2ω1 =k
Таким образом, в рассматриваемом случае гармоники будут сдвинуты по времени на одну и ту же величину к и поэтому сигнал не будет искажен, т. е. форма его останется прежней. Но, естественно, выходной сигнал будет сдвинут относительно входного на время +k (в рассматриваемом случае выходной сигнал будет отставать от входного на время k ).
Определим для рассматриваемого фильтра время замедления: τ(ω) =− dφ(ω)/ dω = k
Таким образом, в рассматриваемом случае время замедления — это время, на которое выходной сигнал будет сдвинут относительно входного.
Если фазочастотная характеристика не будет линейной однородной функцией круговой частоты, то различные гармоники будут сдвинуты фильтром на различные отрезки времени, и поэтому форма сигнала, содержащего не одну гармонику, будет искажаться. Чем ближе фазочастотная характеристика некоторого фильтра к линейной однородной функции (и чем меньше значения времени замедления отличаются от некоторой константы), тем искажения будут меньше.

Из изложенного следует, что частотные характеристики фильтра полностью определяются значением коэффициента K передаточной функции, а также значением ее нулей и полюсов. Нули и полюсы часто изображают в виде точек на плоскости комплексной частоты (s-плоскости), получая так называемую диаграмму нулей и полюсов.
Такая диаграмма вместе с коэффициентом K несет полную информацию о частотных свойствах фильтра. Имея диаграмму нулей и полюсов, легко определить значения модуля и аргумента частотной передаточной функции, т. е. коэффициент усиления и сдвиг по фазе.
Допустим, что некоторый полюс р k расположен на s-плоскости так, как показано на рис. 2.51. 
Пусть круговая частота равна ω1. Тогда для учета полюса р k в знаменатель дроби, определяющей величину |T(jω)|, следует добавить сомножитель, равный длине вектора с началом в полюсе р k и окончанием на мнимой оси с ординатой ω1, а в алгебраическую сумму, определяющую величину arg T(jω), следует добавить слагаемое − φ k, где φ
k— угол, указанный на рисунке.