 Что такое ЦАП?
Что такое ЦАП?
Цифроаналоговые преобразователи (ЦАП) – предназначены для преобразования цифровых сигналов в аналоговые. Такое преобразование необходимо, например, при восстановлении аналогового сигнала, предварительно преобразованного в цифровой для передачи на большое расстояние или хранения (таким сигналом, в частности, может быть звук). Другой пример использования такого преобразования — получение управляющего сигнала при цифровом управлении устройствами, режим работы которых определяется непосредственно аналоговым сигналом (что, в частности, имеет место при управлении двигателями).

Разрешающая способность — величина, обратная максимальному числу шагов квантования выходного аналогового сигнала. Время установления tуст — интервал времени от подачи кода на вход до момента, когда выходной сигнал войдет в заданные пределы, определяемые погрешностью.
Погрешность нелинейности — максимальное отклонение графика зависимости выходного напряжения от напряжения, задаваемого цифровым сигналом, по отношению к идеальной прямой во всем диапазоне преобразования.
Как и рассматриваемые аналого-цифровые преобразователи (АЦП), ЦАП являются «связующим звеном» между аналоговой и цифровой электроникой. Существуют различные принципы построения АЦП.
Схема ЦАП с суммированием весовых токов
На рис. 3.88 приведена схема ЦАП с суммированием весовых токов. 
Ключ S5 замкнут только тогда, когда разомкнуты все ключи S1…S4 (при этом uвых= 0). U0
— опорное напряжение. Каждый резистор во входной цепи соответствует определенному разряду двоичного числа.
По существу этот ЦАП — инвертирующий усилитель на основе операционного усилителя. Анализ такой схемы не представляет затруднений. Так, если замкнут один ключ
S1, то uвых= −U0Roc/ R
что соответствует в первом и нулям в остальных разрядах.

Из вышеизложенного следует, что uвых= − ( U0Roc / R ) · S1 − ( U0Roc / (R/2) ) · S2 – − ( U0Roc / (R/4) ) · S3 − ( U0Roc / (R/8) ) · S4 = = − ( U0Roc / R ) · ( 8S4 + 4S3 + 2S2 + S1)
где Si ,i = 1, 2, 3, 4 принимает значение 1, если соответствующий ключ замкнут, и 0, если ключ разомкнут.
Состояние ключей определяется входным преобразуемым кодом. Схема проста, но имеет недостатки: значительные изменения напряжения на ключах и использование резисторов с сильно отличающимися сопротивлениями. Требуемую точность этих сопротивлений обеспечить затруднительно.
ЦАП на резистивной матрицы R — 2R
Рассмотрим ЦАП на основе резистивной матрицы R — 2R(матрицы постоянного сопротивления) (рис. 3.89). 
В схеме использованы так называемые перекидные ключи S1…S4, каждый из которых в одном из состояний подключен к общей точке, поэтому напряжения на ключах невелики. Ключ S5 замкнут только тогда, когда все ключи S1…S4 подключены к общей точке. Во входной цепи использованы резисторы всего с двумя различными значениями сопротивлений.

Пусть каждый из ключей S1…S4 подключен к общей точке. Тогда, как легко заметить, напряжение относительно общей точки в каждой следующей из точек «a»…«d» в 2 раза больше, чем в предыдущей. К примеру, напряжение в точке «b» в 2 раза больше, чем в точке «а» (напряжения Uа, Ub, Uc и Ud в указанных точках определяются следующим образом:
Ua = U0
Uc = U0 / 2
Ub = U0 / 4
Ud = U0 / 8
Допустим, что состояние указанных ключей изменилось. Тогда напряжения в точках «a»…«d» не изменятся, так как напряжение между входами операционного усилителя практически нулевое.
Из вышеизложенного следует, что:
uвых= − ( U0Roc / 2R ) · S4 − ( (U0/2) Roc / 2R ) · S3 – ( (U0/4) Roc / 2R ) · S2 − ( (U0/8) Roc / 2R ) · S1 = − ( U0Roc/ 16R) · ( 8S4+ 4S3+ 2S2 + S1)
где Si , i = 1, 2, 3, 4 принимает значение 1, если соответствующий ключ замкнут, и 0, если ключ разомкнут.
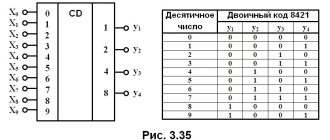
ЦАП для преобразования двоично-десятичных чисел
Рассмотрим ЦАП для преобразования двоично-десятичных чисел (рис. 3.90).

Для представления каждого разряда десятичного числа используется отдельная матрица R − 2R (обозначены прямоугольниками). Z0…Z3 обозначают числа, определенные состоянием ключей каждой матрицы R − 2R.

 Из анализа следует, что
Из анализа следует, что
U2 = U1 · [ ( R||9R) / (8,1R + R||9R) ]
R||9R = (R · 9R) / (R + 9R) = 0,9R
Следовательно, U2 = 0,1 U1. С учетом этого получим?
uвых= − ( U0Roc / 16R ) · 10−3 ( 103 · Z3 + 102 · Z2 + 10 · Z1 + Z0)
Наиболее распространенными являются ЦАП серий микросхем 572, 594, 1108, 1118 и др. В табл. 3.2 приведены…
Параметры ЦАП












Спасибо за статью – помогла разобраться