Отстройка дифференциальной защиты силового трансформатора от бросков тока намагничивания (БТН) — это одна из сложнейших проблем при разработке алгоритма ее функционирования. Эта проблема заключается в том, что ток намагничивания потребляется внутри зоны защиты, вследствие чего режим БТН имеет много общего с режимом внутреннего короткого замыкания (КЗ). Искажения вторичных токов вследствие насыщения трансформаторов тока (ТТ) во время переходных процессов существенно усугубляют проблему. Поэтому алгоритмы функционирования дифзащит трансформаторов должны предусматривать специальные средства, выявляющие в дифференциальном токе отличительные признаки качественного характера. Считается, что в дифференциальном токе в режиме БТН высшие гармонические составляющие содержатся в большей степени, чем при внутренних КЗ.
Поэтому нашло широкое распространение торможение гармоническими составляющими дифференциального тока (преимущественно второй гармоникой) в качестве средства отстройки дифзащит трансформаторов от БТН.
Пригодность такого средства отстройки обосновывается результатами гармонического анализа дифференциального тока в режиме БТН с учетом искажений, о которых имеются публикации.
Однако публикации о гармоническом анализе дифференциальных токов при внутренних КЗ, причем именно искаженных токов вследствие насыщения ТТ, практически отсутствуют. Поэтому целью настоящей работы является исследование гармонических слагающих дифференциального тока и, как следствие, оценка эффективности самых распространенных способов отстройки от БТН.
Принципы торможения высшими гармониками можно разделить на две группы: торможение величиной (амплитудой) высшей гармонической составляющей и торможение коэффициентом гармоники (относительной гармоникой). Под коэффициентом гармоники понимается отношение амплитуды высшей гармоники к амплитуде первой гармоники; это отношение обычно выражается в процентах. Основным недостатком торможения величинами высших гармоник является то, что при изменении величины токового сигнала при одном и том же режиме изменяются и величины гармонических слагающих. При искажении дифференциального тока вследствие насыщения ТТ резко изменяется его форма, а значит, и его спектр. В этом отношении коэффициент гармоник имеет преимущество перед их амплитудами, заключающееся в следующем. С изменением токового сигнала по величине, а может даже и по форме, в каком-либо одном режиме величины гармонических слагающих изменяются в какой-то мере пропорционально друг другу. Значит, коэффициенты гармоник в этом режиме претерпят значительно меньшие изменения, чем просто величины гармонических слагающих.
Во многих современных цифровых защитах силовых трансформаторов отстройка от БТН основывается именно на использовании коэффициентов гармоник, а не просто их величин. В литературе и технических описаниях дифференциальных защит трансформаторов, как правило, не приводится точного описания способов отстройки реле от БТН с помощью торможения высшими гармониками. Максимум, что в редких случаях указывается, это величины коэффициентов гармоник, по которым следует отличать внутреннее КЗ от БТН. Например, в защите, описанной в, в качестве такой уставки принято значение коэффициента второй гармоники 17,7 %, в защитах RET316 и RET521 — 12 %, в цифровой защите ШЭ1111 фирмы ЭКРА — 10 %. Но кроме самих коэффициентов гармоник очень важным фактором в эффективности отстройки дифзащиты оказывается способ выделения гармонических слагающих.
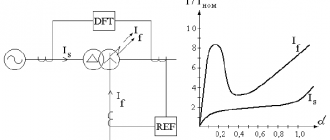
В работе проведено сопоставление многих применяемых способов, и в ней указывается, что дискретное преобразование Фурье является самым точным и самым эффективным для отстройки дифзащиты трансформатора от БТН.
Приведенные значения коэффициентов высших гармоник, выявленных методом преобразования Фурье, для различных искаженных кривых дифференциального тока в режиме БТН.
Значения коэффициентов гармоник для приведенных случаев БТН лежат в очень широких пределах: постоянная слагающая — от 4 до 73 %; вторая гармоника — от 17 до 102 %; третья гармоника — от 1 до 39 %.
При проведении гармонического анализа дифференциальных токов в переходных процессах внутренних КЗ применялась модель трехфазных групп ТТ «звезда» и «треугольник», созданная в пакете MatLab [4]. Кривая намагничивания магнитопроводов в этой модели задана в виде усредненной монотонно изменяющейся характеристики (без учета гистерезиса), что обеспечивается функциями ускоренной интерполяции пакета MatLab. Для определения величин гармонических слагающих используется функция «fft», реализующая алгоритм быстрого преобразования Фурье.
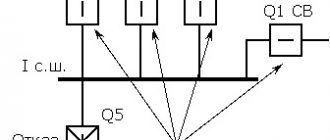
При исследованиях моделировались внутренние КЗ для защиты блочного двухобмоточного трансформатора ТД 80000/220/10. Проведенные исследования справедливы (применимы) для дифзащиты любого силового трансформатора, так как характер искажений токов в группах трансформаторах тока «звезда» и «треугольник» слабо зависит от их типа. На рис. 1 приведен пример внутреннего трехфазного КЗ с двухсторонним питанием.
Начальные условия для этого случая принимались следующими:
- кратности тока КЗ с обеих сторон равны 4;
- остаточные индукции для группы ТТ «звезда» 1,0, 0,2 и 0,8 Тл для фаз А, В и С соответственно,
- для группы ТТ «треугольник» — 1,0, 1,0 и 1,2 Тл для фаз А, В и С соответственно.
Для каждой фазы в верхней части рисунка показаны первичные и вторичные токи для стороны низшего напряжения с группой ТТ «звезда», в средней части — для стороны высшего напряжения с группой ТТ «треугольник», в нижней части рисунка — дифференциальный ток.
На рис. 2 приведен пример внутреннего трехфазного КЗ, но с односторонним питанием со стороны низшего напряжения. Поэтому на рис. 2 приведены только первичные и вторичные токи плеча с группой ТТ «звезда»; в таком случае дифференциальный ток в каждой фазе равен вторичному току.
Величины относительных гармонических слагающих в процентах указаны в табл. 1 и 2. Здесь продемонстрированы такие случаи внутренних КЗ, при которых коэффициенты второй гармоники оказываются наибольшими, хотя не максимально возможными.
Более высокие значения относительной второй гармоники могут наблюдаться при гораздо менее вероятных искажениях вторичных токов, а приведенные примеры искаженных токов являются наиболее характерными.
Следует отметить, что в обоих приведенных случаях в фазе В ток практически не искажается, кроме того, первичный ток не содержит апериодической слагающей, поэтому коэффициенты высших гармоник в ней составляют единицы процентов и приводить их точные значения не имеет смысла.
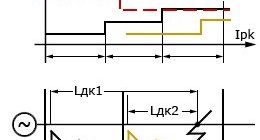
На рис. 3 показан один из возможных режимов БТН при включении силового трансформатора на холостой ход со стороны обмотки НН, имеющей схему соединения «треугольник», а вторичные обмотки ТТ — схему «звезда». Коэффициенты гармонических слагающих для дифференциального тока в этом режиме приведены в табл. 3. При анализе результатов исследований видно, что диапазоны величин относительных гармонических слагающих, характерных внутренним КЗ и режиму БТН, очень сильно пересекаются. Величины коэффициента второй гармоники, появляющейся при внутренних КЗ, могут в несколько раз превышать принятые уставки в современных дифференциальных защитах, по которым они идентифицируют бросок тока намагничивания. Особое внимание следует уделить коэффициенту второй гармоники в первом периоде, так как именно с первого периода начинается выявление БТН, а в первом периоде ТТ еще не столь глубоко насыщены, как в последующих периодах.
При таких обстоятельствах в режиме БТН вторая гармоника может оказываться больше, чем при внутренних КЗ. Но из таблиц 1 и 2 видно, что при внутренних КЗ относительная вторая гармоника уже в первом периоде может существенно превышать принятые в защитах трансформаторов уставки.
В таких случаях внутренних КЗ возможны задержки в срабатывании защит, поскольку в самом начале переходного процесса возможно неверное распознавание режима работы защищаемого трансформатора. Во втором и последующих периодах насыщение ТТ усиливается, что влечет к увеличению высших гармонических слагающих, а вследствие этого задержка в срабатывании защиты будет продолжаться.
Наоборот, в случае апериодического БТН, при отсутствии искажений в дифференциальном токе во время первого и второго периодов, относительная вторая гармоника может быть на уровне 14-15% (см. табл. 3, фаза А), что может оказаться только лишь на уровне или даже ниже уставки.
Относительные значения третьей и четвертой гармоник при БТН оказываются несколько большими, чем при внутренних КЗ, но провести четкую границу по их значениям между этими двумя режимами также очень сложно. Относительные значения пятой и шестой гармоник как при внутренних КЗ, так и при БТН составляют единицы процентов, поэтому они также не представляют никакой ценности для отстройки от БТН. В заключение можно констатировать низкую эффективность любых способов отстройки от БТН, которые используют высшие гармонические слагающие.
Низкая эффективность таких способов также указывается в работе.
Если гармонические слагающие выделяются из выпрямленного дифференциального тока или из его производной по времени, то такой подход вносит дополнительные сложности и дополнительно снижает устойчивость функционирования дифференциальной защиты трансформатора.
Источник:Журнал “ЭЛЕКТРО. Электротехника. Электроэнергетика. Электротехническая промышленность.” № 3 за 2007 год.
Автор: Купарев Михаил Анатольевич, к.т.н., доцент Новосибирского государственного технического университета.
