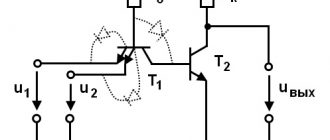
Рассмотрим влияние ООС на примере усилителя, охваченного последовательной обратной связью по напряжению (рис. 2.10).
Рассмотрим влияние ООС на примере усилителя, охваченного последовательной обратной связью по напряжению (рис. 2.10).
В структурную схему входит цепь прямой передачи и цепь обратной связи (цепь обратной передачи). Предполагается, что указанные цепи линейные. На усилитель с обратной связью подается внешний синусоидальный входной сигнал uвх1, а на цепь прямой передачи — сигнал
uвх2. Цепь прямой передачи характеризуется комплексным коэффициентом усиления по напряжению Кu (коэффициентом прямой передачи):
Ќu= Úвых / Úвх2 где Úвх2, Úвых − соответственно комплексные действующие значения напряжений uвх2и uвых. Цепь обратной связи характеризуется комплексным
коэффициентом обратной связи β:
β′ = Úос / Úвых
где Úос — комплексное действующее значение напряжения обратной связи uос. Коэффициент усиления усилителя, охваченного обратной связью.
Этот коэффициент К uос определяется по формуле:
Ќuос= Úвых / Úвх1
где Úвх1 — комплексное действующее значение напряжения uвх1. Легко заметить, что Úвх2 = Úвх1 – Úос
Úвх1 = Úвх2 + Úос Поэтому Ќuос= Úвых/ Úвх1=Ќu· Úвх2/ ( Úвх2+ Úос) ==Ќu· Úвх2/ ( Úвх2+ β′ · Úвых) =Ќu· Úвх2/ ( Úвх2+ β′ ·Ќu· Úвх2) == Ќu/ ( 1 +β′ · Ќu) Таким образом,Ќuос= Ќu/ ( 1 +β′ · Ќu)Ќuос≈ 1 /β′
Величину 1 +β′ · Ќu называют глубиной обратной связи (коэффициентом грубости схемы), а величинуβ′ · Ќu называют петлевым усилением. Если глубина обратной связи достаточно велика, то |β′ · Ќu| >> 1.
Отсюда можно сделать следующий очень важный вывод: если глубина отрицательной обратной связи достаточно велика, то коэффициент усиления усилителя, охваченного обратной связью Ќ uос, зависит только от свойств цепи обратной связи и не зависит от свойств цепи прямой передачи.

Даже если глубина обратной связи не настолько велика, что можно пренебрегать единицей в выражении 1 + β′ · Ќu, отрицательная обратная связь, как можно показать, уменьшает нестабильность коэффициента Ќuос.Важно уяснить, что сделанный вывод справедлив независимо от того, какие дестабилизирующие факторы влияют на изменение величины Ќu (температура, уровень радиации и т. д.).
Частотные характеристики усилителя, охваченного обратной связью.
Если рассуждать формально, то при наличии частотных характеристик для Ќuи β′ частотные характеристики для Ќu осоказываются однозначно определенными выражением Ќuос= Ќu/ 1 +β′ · Ќu)Тем не менее, очень поучительно более детально рассмотреть вопрос влияния отрицательной обратной связи на частотные свойства усилителя.
Пусть коэффициенты Ќuи β′ являются вещественными. Тогда и коэффициент Ќuос— вещественный. Будем для этого случая использовать обозначения Ќu, β′ и Ќuос. Пусть в некотором частотном диапазоне коэффициент Ќ uизменяется в пределах от 10000 до 1000 (на 90% по отношению к значению 10000), а коэффициент β′ является постоянным, β′ = 0,1. Тогда в соответствии с формулой для Ќu с окажется, что Ќuос будет изменяться в пределах от 9,99 до 9,9 (примерно на 1%). Таким образом, изменение коэффициента усиления после введения отрицательной обратной связи станет значительно меньшим.
Важно уяснить, что если все же необходимо повысить коэффициент усиления до 10000, то и в этом случае использование отрицательной обратной связи значительно улучшит стабильность.
Пусть для получения большого коэффициента усиления использованы 4 включенных последовательно описанных усилителя, охваченных отрицательной обратной связью. Тогда в рассматриваемом диапазоне частот общий коэффициент усиления будет изменяться в пределах от 9960 (9,99 · 9,99 · 9,99 · 9,99) до 9606 (9,9 · 9,9 · 9,9 · 9,9).
Изменение составит 3,6% ((9960 − 9606) / 9960 · 100%). Это, очевидно, значительно меньше 90%.
В том диапазоне частот, в котором выполняется условие |β′ · Ќu| >> 1, коэффициент Ќu осможно определить из выражения| Ќuос| = 1 / |β′ |
В первом приближении можно считать, что единицей можно пренебречь при условии, что 1 < |β′ · Ќu| Отсюда получаем |Ќu| > 1/ |β′ |
Пусть в качестве цепи прямой передачи используется рассмотренный выше операционный усилитель К140УД8, а в качестве цепи обратной связи — делитель напряжения, причем β=β ′ = 0,1 (рис. 2.11). 
Легко заметить, чтоÚос = Úвых · 0,1Таким образом, для этой схемы действительно β≈Uос/Uвых= 0,1
В соответствии с полученным выше неравенством можно, в первом приближении, считать, что | Ќuос| = 1/β= 10 в том диапазоне частот, в котором | Ќu| > 10. 

Входное сопротивление усилителя, охваченного обратной связью.
Обратимся к структурной схеме усилителя с последовательной отрицательной обратной связью (рис. 2.13). 
Обозначим через Zвх входное комплексное сопротивление цепи прямой передачи:
Zвх = Úвх2 / Íвx где Íвx − комплексное действующее значение тока Iвx.
Найдем входное комплексное сопротивление Zвх ос усилителя, охваченного обратной связью:
Zвх ос =Úвх1/Íвx
Получим Zвх ос = Úвх1 / Íвx == ( Úвх2 + Úос ) / Íвx = ( Úвх2 + β′ · Úвых ) / Íвx == ( Úвх2 + Úвх2 · β′ · Ќ u) / Íвx = ( Úвх2 / Íвx ) · ( 1 + β′ · Ќu) == Zвх · ( 1 + β′ · Ќu)
Таким образом, Zвх ос = Zвх · ( 1 + β′ · Ќ u) Пусть коэффициенты Ќ u и β′ являются вещественными (Ќu= Кu и β′ = β).
Отсюда следует, что последовательная отрицательная обратная связь увеличивает входное сопротивление по модулю. Практически всегда это является положительным фактором.
Выходное сопротивление усилителя, охваченного обратной связью.
Обозначим через Zвых и Zвых ос соответственно выходное комплексное сопротивление цепи прямой передачи и выходное комплексное сопротивление усилителя, охваченного обратной связью. По определению Zвых = − ∆Úвых / ∆Íвых где ∆Úвых, ∆Íвых — приращения комплексных действующих значений соответственно напряжения Uвыхи тока Iвых. При этом предполагается, что обратная связь отключена (например, выход цепи обратной связи закорочен).
Также предполагается, что Uвхl = const, а изменение величин Uвых и Iвых вызвано изменением сопротивления нагрузки.
По определению Zвых ос = − ∆Úвых / ∆Íвых но при этом предполагается, что обратная связь действует и что Uвхl = const.
В этом случае причиной возникновения приращения ∆Úвых является не только падение напряжения на выходном сопротивлении Zвых, но и появление приращения ∆Úвых = − ∆Íвых · Zвых – ∆Úос · Ќ u где ∆Úос − комплексного действующего значения напряжения Uос.
Следовательно, Ќuос= Ќu/ ( 1 + β′ · Ќu) Знаки «минус» использованы потому, что и увеличение тока Iвых, и увеличение напряжения Uо свызывают уменьшение напряжения Uвых.
∆Úвых = −∆Íвых ·Zвых− ∆Úвых · β′ · Ќu
Отсюда с учетом, что ∆Úос = ∆Úвых · β′получим ∆Úвых= −∆Íвых· Zвых/ ( 1 +β′ ·Ќu) В соответствии с этимZвых ос = − ∆Úвых / ∆Íвых =Zвых/ ( 1 + β′ · Ќu)
Пусть коэффициенты Ќu и β′ являются вещественными. Тогда, очевидно, отрицательная обратная связь по напряжению уменьшает выходное сопротивление усилителя. Очень часто это является положительным фактором.