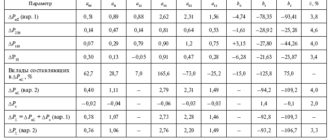
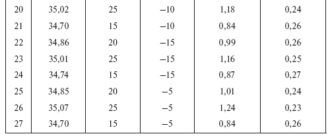
Характеристики графиков нагрузки
Известно большое количество приближенных формул для определения значений τ и 2 ф k (гл. 2), которые можно разбить на две группы:
- формулы, выводимые для графика нагрузки по продолжительности, описываемого принятой автором математической моделью (прямой линией, выпуклой или вогнутой кривой, приведенного к двухступенчатому виду и т. п.);
- формулы, полученные при обработке вариантных расчетов τ и 2 ф k для графиков различных конфигураций или для типовых графиков нагрузки.
Для оценки погрешностей известных из литературы эмпирических формул расчета τ авторами [29] проведены сопоставительные расчеты для всех возможных конфигураций графика нагрузки по продолжительности с дискретностью 0,1 по обеим осям (рис. П1.1).

Рис. П1.1. Графики нагрузок по продолжительности для нагрузочных узлов: 1 – график с kз = 0,19 и kмин = 0,1; 2–4 – графики с kз = 0,49 и kмин = 0,1; 5 – график, соответствующий равновероятному распределению нагрузки
Количество вариантов графиков при такой дискретности составляет 48 620 в диапазоне kз от 0,19 (график 1) до 1 (полностью заполненный график). Для каждого варианта вычислялось точное значение τ по формуле (2.4) и значения τ по 13 эмпирическим формулам, описанным ниже. В результате расчетов определены систематические и случайные погрешности каждой из 13 формул как в целом по всем вариантам графиков, так и по трем зонам значений kз : 0,19–0,4; 0,4–0,7 и 0,7–1, в которые попало соответственно 2 283, 36 941 и 9 396 вариантов графиков.
Более сложный вид имеют формулы, использующие два параметра: kз и kмин (все формулы преобразованы в сопоставимый вид):
формулы (2.19) – (2.20). Величина τ, определяемая по ним, далее обозначена как τ1 ;
формулы, приведенные в [30] – [32]:

Остальные восемь формул приведены непосредственно в табл. П1.1. Ссылки на авторов формул для τ6 – τ11 приведены в [34] и [35].
Таблица П1.1
Расчетные формулы для τ и их погрешности


Формула для τ12 соответствует графику, представленному прямой линией (линия 5 на рис. П1.1) и отражающего предположение о равновероятном нахождении нагрузки в диапазоне от максимального до минимального значений. Для такого графика значение kмин связано с kз соотношением kмин = 2 kз – 1, поэтому достаточно задания только одного параметра, а значение τ12 равно значению τ1 при λ = 1. Очевидно, что такое представление графика можно использовать только в диапазоне kз ≥ 0,5, так как при меньшем его значении правая точка графика опускается ниже нуля. При kз = 0,5 значение τ12 = 1/3 , а коэффициента формы графика

В отечественной литературе до недавнего времени наиболее часто использовалась формула для τ6 . В 1940 г. проф. А. М. Заславский на основе ручной обработки многочисленных графиков получил зависимость между средним и среднеквадратичным током, соответствующую данной формуле. В 1948 г. доц. В. В. Кезевич простым преобразованием выражения А. М. Заславского записал формулу для τ 6. Поэтому она часто называется формулой Кезевича.
Авторы [29] осуществили более объемный перебор всех возможных графиков нагрузки, используя возможности современной вычислительной техники, которой не располагал проф. А. М. Заславский. В результате получена более точная формула, приведенная в табл. П1.1 под обозначением τ13 . При полученных значениях коэффициентов 0,34 (∼ 1/3) и 0,66 (∼ 2/3) формулы для τ13 и 2 ф k могут быть записаны в следующем виде:
![]()
Погрешности расчета 2 ф k имеют такие же значения, что и погрешности расчета τ, так как величины τ и 2 ф k функционально связаны между собой множителем 2 з k (2.6). Поэтому далее рассматриваются только формулы для расчета τ. В табл. П1.1 систематическая погрешность обозначена ∆э , случайная (+/–) – δэ . Случайная погрешность дана для уровня вероятности 0,95 (удвоенное значение среднеквадратичной погрешности).
Анализ результатов расчетов позволяет сделать следующие выводы:
- случайные погрешности всех формул снижаются по мере приближения к единице, что не удивительно, так как при увеличении kз сокращается диапазон разнообразия конфигураций графиков, а при kз = 1 все формулы приводят к значению τ = 1. В диапазоне kз = 0,7 – 1,0 наилучшие результаты дают формулы для τ1 , τ2 и τ4 , которые используют два параметра: kз и kмин;
- наименьшую случайную погрешность при использовании во всем диапазоне kз обеспечивает формула для τ1 (10,8 %), незначительно уступает ей формула для τ4 (11,4 %);
- случайные погрешности формул, использующих только значение kз , ненамного выше – у семи таких формул (τ6 , τ7 , τ9 – τ13 ) они находятся на уровне (13 – 13,6) %;
- систематические погрешности в принципе могут быть учтены в расчете поправочными коэффициентами, поэтому они имеют меньшее значение для оценки точности методов, однако их непостоянство делает такую корректировку несколько неудобной. С этих позиций предпочтительнее формула для τ13, которая имеет практически нулевую систематическую погрешность.
Зависимости случайных погрешностей формул для τ6 , τ7 , τ9 – τ11 и τ13 от kз хорошо аппроксимируются выражениями, %:
которые могут использоваться для оценки интервалов неопределенности расчетных значений потерь электроэнергии в конкретном расчете.
Очевидно, что два параметра (kз и kмин ) не могут однозначно характеризовать внутреннюю структуру графика – в противном случае погрешности зависимостей были бы равны нулю. На рис. П1.1 изображены графики 2, 3 и 4, имеющие одинаковые значения kз = 0,49 и kмин = 0,1. Значения τ0 , вычисленные для них по формуле (2.4), составляют соответственно 0,327; 0,295 и 0,373. При использовании любой эмпирической формулы для этих графиков будет получено одно значение τ, так как формулы исходят из значений kз и kмин, а они одинаковы для всех трех графиков. Тем более не может полноценно характеризовать структуру графика один параметр. Проведенные исследования позволяют утверждать, что погрешность примерно 13 % можно считать «врожденной» погрешностью эмпирических формул, использующих только значение kз . Использование дополнительно к kз значения kмин несущественно снижает погрешность (до 10,8 %). Вместе с тем значения kмин имеют, как правило, меньшую достоверность, чем значения kз , поэтому незначительное уточнение, получаемое при использовании формул с двумя параметрами, может нивелироваться неточностью значения kмин.
Графики нагрузки сетей 6–10 кВ и выше по природе являются графиками смешанной нагрузки и имеют самые различные конфигурации, поэтому для них практически невозможно использовать понятие типа графика. Задание типа графика уже предполагает наличие данных о его конфигурации, а в этом случае целесообразно пользоваться непосредственно формулой (2.4). При отсутствии таких данных задание типа графика может быть осуществлено только субъективно. Поэтому в практических расчетах целесообразно использовать расчетные формулы с объективной характеристикой – kз .
Учет отличия коэффициентов формы графиков активной мощности и полного тока
Коэффициент формы графика нагрузки, используемый при расчете потерь электроэнергии, иногда вычисляют по графику полного тока. Конфигурации графиков активной мощности и тока отличаются друг от друга вследствие учета в значении тока реактивной составляющей нагрузки. Однако график реактивной нагрузки обычно более плотный, чем активной – из-за значительной постоянной составляющей (холостой ход).
Точный учет этого фактора предполагает запись формулы (2.46) с выделением в ней составляющих потерь от передачи активной WP 350 и реактивной WQ энергии, при расчете каждой из которых учитываются коэффициенты формы графиков P и Q:
![]()
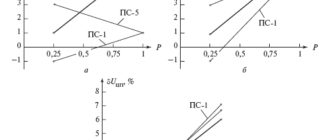
При использовании в формуле (2.46) вместо 2 ф k величины 2 фP k погрешность вычисления потерь отражается формулой, %:

При неизменном значении tg ϕ на всех ступенях графика а = 1 и δР = 0. Так как график реактивной мощности более ровный, чем активной, а < 1 и погрешность δР имеет положительный характер. Из формулы (П1.6) следует также очевидный вывод, что чем меньше tg ϕ, тем меньше погрешность (уменьшается удельный вес составляющей потерь, определяемой по не вполне корректному коэффициенту формы).
Погрешность использования в формуле (2.46) величины 2 фI k вместо 2 ф k определяется по формуле:

Очевидно, что знаменатель формулы (П1.7) по определению положителен и знак погрешности зависит от знака числителя. При одинаковом tg ϕ на всех ступенях графика нагрузки 222 ффф PQI kkk = = . При этом bP = bQ = 1 и δI = 0.
Принимая соотношение
![]()

Для сетей 0,4 кВ конфигурации графиков активной и реактивной мощности практически совпадают (из-за отсутствия потерь холостого хода), поэтому 222 ффф PQI kkk = = .
Приняв для сетей 6– 20 кВ средние значения tg ϕ = 0,6 и с = 1,3, вычислив значения a, bP и bQ и подставив их в (П1.6) и (П1.7), получим δP = 2,2 % и δI = –1,1 %. Полученные цифры показывают, что при использовании коэффициента формы, рассчитанного по графику активной мощности, потери завышаются в среднем на 2,2 % и к расчетным значениям потерь надо применять поправочный коэффициент 1/1,022 = 0,98. При расчете коэффициента формы по графику тока потери несколько занижаются и значение поправочного коэффициента составляет 1/0,989 = 1,01.
При использовании метода наибольших потерь данные коэффициенты подставляются в знаменатель формул, так как при уменьшении коэффициента заполнения графика коэффициент формы увеличивается, а τ уменьшается.
Кроме рассмотренного фактора на расчетное значение потерь влияет описанная в п. 5.5.2 погрешность неадекватности отражения коэффициентом формы графика головного участка потерь во всех элементах сети, каждый из которых имеет свой график нагрузки. Среднее значение коэффициента неадекватности для сетей 6–20 кВ составляет 1,01. С учетом этого поправочные коэффициенты в формуле расчета потерь повысятся на 1 % и составят соответственно 0,99 и 1,02.
Характеристики режимов напряжения
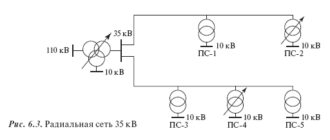
Рассмотрим режимы напряжения в ЦП и в узлах идеализированной радиальной сети с равномерным распределением нагрузок по ее длине. Для простоты не учитываем емкостную генерацию линий. Суточный график нагрузки примем трехступенчатым с относительными нагрузками на ступенях, равными 1,0; 0,8 и 0,6, с одинаковыми продолжительностями ступеней и напряжениями в ЦП U1 = = 115 кВ; U2 = 112 кВ и U3 = 109 кВ. Напряжения в узлах сети по мере их удаления от ЦП снижаются в соответствии с линейной зависимостью. На рис. П1.2 эпюры напряжения в рассматриваемых режимах отображаются линиями U1 – 1, U2 – 2 и U3 – 3.
Очевидно, что для учета различия напряжения в ЦП на ступенях графика в расчетном режиме необходимо использовать некоторое эквивалентное напряжение в ЦП, находящееся между значениями U1 и U3 . Ясно также, что оно должно быть меньше U1 , представляющего собой напряжение в режиме максимальной нагрузки.

Расчетное напряжение в ЦП для каждого из трех описанных выше методов определяется из равенства:

Обозначив первую сумму, соответствующую учету фактических режимов напряжения на каждой ступени графика, через MU, получим следующие выражения для расчетного напряжения в ЦП в каждом из методов:


Анализируя уравнение (П1.12) с учетом соотношения (2.6), нетрудно заметить, что все три уравнения (П1.13) – (П1.15) приведут к одинаковому результату, если использовать точные значения τ0 и 2 ф k , рассчитываемые по формулам (2.4) и (2.5). Для рассматриваемого графика с округлением до четвертого знака после запятой τ0 = 0,6667, а 2 ф k = 1,0417. Подставив эти значения в (П1.13) и (П1.15), получим Uр1 = Uр2 = Uр3 = 112,9 кВ. Данное значение несколько выше среднего, равного 112 кВ, что логично, так как напряжение режима наибольших потерь более значимо для правильного определения интегрального показателя: потери в этом режиме составляют наибольшую долю в суммарных потерях. При использовании приближенных значений τ0 и 2 ф k , рассчитываемых по формулам (2.16) и (2.17), значение Uр1 = Uр2 будет немного отличаться от значения Uр3. В данном случае это отличие несколько компенсирует погрешности расчета τ0 и 2 ф k по эмпирическим формулам.
При проведении расчетов методом 3 использовать значение Uр3 нецелесообразно. Этот метод предполагает отдельный расчет каждого режима, поэтому следует использовать фактические значения напряжения в ЦП в рассчитываемых режимах, а не некое эквивалентное, одинаковое для всех режимов значение. При использовании этого метода можно одновременно учесть и различия рабочих схем сети в каждом режиме.
Однако определением эквивалентного напряжения в ЦП по его значениям в различных режимах проблема не исчерпывается. Использование значений Uр1 и Uр2, определенных таким способом, предполагает, что эпюра напряжений во всех нерасчетных режимах имеет такой же наклон, как и в расчетном режиме. На рис. П1.2 она отображается линиями U2 – 2(1) и U3 – 3(1), которые имеют больший наклон, чем реальные эпюры для этих режимов. При постоянном напряжении в ЦП, равном U1 , эпюры напряжений в двух других режимах отображаются линиями U1 –1(2) и U1 –1(3). Напряжения на удаленных участках в этих режимах выше, чем в режиме максимума нагрузки, что приводит к уменьшению нагрузочных потерь и должно выражаться в некотором увеличении расчетного напряжения в ЦП по сравнению с напряжением, определяемым при учете напряжений только на шинах самого ЦП.
При учете этого аспекта следует иметь в виду, что плотность распределения потерь по длине линии неодинакова; это приводит к неодинаковой весомости учета реальных напряжений на разных участках линии. Для радиальных линий характерно резкое снижение плотности потерь по мере удаления от ЦП. Обычно до 70 % суммарных потерь приходится на несколько головных участков линии, по которым проходит мощность суммарной нагрузки. По мере отборов мощности протекающая нагрузка снижается, ее квадрат соответственно снижается еще больше. Снижение сечения проводов лишь частично компенсирует влияние на потери уменьшающейся нагрузки. Кроме того, при выборе сечения провода существуют ограничения по минимальному сечению, определяющему механическую прочность провода, что не позволяет уменьшать сечение пропорционально снизившейся нагрузке. В результате плотность тока в проводах по мере удаления от ЦП снижается, приводя к уменьшению удельных потерь.
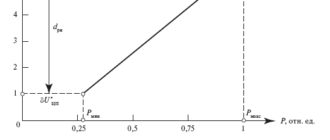
На рис. П1.2 приведены качественные характеристики распределения потерь по длине линии в каждом режиме – dP1 , dP2 и dP3 . Начальные точки этих кривых соответствуют квадратичному соотношению потерь при различных нагрузках режимов. Разделив условно длину линии на k зон и обозначив долю потерь, приходящуюся на каждую зону через dj , определим коэффициент увеличения расчетного напряжения в ЦП из равенства:

Если принять в рассматриваемом примере деление сети на три зоны с относительными длинами 0,3; 0,3 и 0,4 (расстояние до начала зон 0; 0,3 и 0,6 соответственно), распределением потерь по ним, равным d1 = 0,5; d2 = 0,4 и d3 = 0,1 и максимальные потери напряжения ∆U1 = 10 %, то по формуле (П1.17) получим Uр1 = UЦП; Uр2 = 0,97UЦП; Uр3 = 0,94UЦП. Подставляя эти значения в формулу (П1.16), получим kU = 1,018.
Изложенный подход к определению расчетного напряжения в ЦП носит скорее теоретический характер. Учитывая ограниченную достоверность всех данных, используемых в расчетах потерь электроэнергии, допустимо определять расчетное напряжение в ЦП по эмпирической формуле (2.33).
Для рассматриваемого примера kз = 0,8. Значение корня в формуле (2.33) равно 112,6 кВ. Это значение отражает эквивалентное напряжение на шинах ЦП, определяемое более точно по формуле (П1.17). Учет снижения напряжения в узлах сети отражается сомножителем в скобках, равным для данного примера 1,02. В результате расчетное напряжение в ЦП, которое следует использовать в режиме максимальной нагрузки для более точного расчета нагрузочных потерь электроэнергии Uр = 1,02 · 112,6 = 114,85 кВ. Близость этого напряжения к напряжению в ЦП в режиме максимальной нагрузки следует рассматривать лишь в контексте данного примера.
Очевидно, что при меньших значениях ∆Uмакс расчетное напряжение будет ниже (нагрузочные потери выше), а при меньших значениях kз – выше. Рассмотренные факторы влияния фактических режимов напряжения в сети на потери электроэнергии действуют в противоположных направлениях. При этом следует иметь в виду, что потери мощности в режиме максимальной нагрузки, определенные при задании такого расчетного напряжения, будут несколько не соответствовать потерям, определенным при фактическом напряжении в максимум нагрузки, хотя нагрузочные потери электроэнергии за расчетный период определяются более точно.
На потери холостого хода изменение напряжения действует в обратном направлении. Расчетное напряжение в ЦП для этих потерь определяют по формуле (2.34). Для условий примера оно составит 114,3 кВ. С позиции более точного расчета потерь электроэнергии правильно было бы рассчитывать два режима с разными напряжениями в ЦП, по одному из которых определять нагрузочные потери, а по другому – потери холостого хода. Если же рассчитывается один режим, то расчетное напряжение в ЦП необходимо определять как взвешенное по формуле (2.35).