Аналитический способ определения начальной расчетной длины рабочей части кольцевого образца при растяжении

Карагерги Р.П., Евсеев М.В., Барсанова С.В., Козлов А.В. (АО «ИРМ»,  Заречный, Россия), Макеев С.А. («СибАДИ», Омск, Россия)

Введение

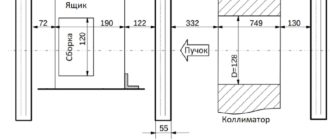
Одним из традиционных методов исследования механических свойств тонкостенных полых труб малого диаметра, применяемых в качестве оболочек тепловыделяющих элементов активной зоны ядерного реактора, является метод испытания кольцевых образцов на растяжение [1–3]. Данным методом определяют механические характеристики применяемых материалов в поперечном направлении, в котором действуют рабочие усилия при эксплуатации оболочечных труб под внутренним давлением. Суть метода заключается в одноосном растяжении кольцевого образца на полуцилиндрических опорах с доведением его до разрушения (рис. 1). Во время испытания записывают диаграмму растяжения в координатах перемещениенагрузка (P), по которой, аналогично стандарту [4], графическим способом рассчитывают кратковременные механические характеристики материала, такие как предел прочности, предел текучести условный и относительное остаточное удлинение после разрыва.

  Рис. 1. Схема растяжения кольцевого образца на опорах до деформации

Данный вид механических испытаний наряду с преимуществами (простота изготовления образцов, экспрессность метода) обладает рядом недостатков. Один из них – сложность учета деформации образца на опорах, а именно при расчете начальной расчетной длины рабочей части образца для определения относительного остаточного удлинения после разрыва.

Исследование деформации кольцевого образца на полуцилиндрических опорах является актуальной задачей для оценки механических свойств металлических труб различных типоразмеров, изготовленных из современных материалов [5–7].

 

1. Методика определения относительного остаточного удлинения кольцевого образца

Относительное остаточное удлинение кольцевого образца определяют графическим способом по диаграмме растяжения [3, 4] и вычисляют по формуле:

(1) где l0 – начальная расчетная длина образца, мм;   lк – конечная расчетная длина образа после разрыва, мм.

Начальную расчетную длину рабочей части l0 для кольцевого образца вычисляют перед проведением испытания по формуле [3, 8–11]:

(2) где Dср – средний диаметр образца, мм;

Dз – диаметр опор захвата, мм;

a – толщина стенки образца, мм;

k – коэффициент деформации, определенный эмпирическим путем [9–11], равен 0,5 для сталей, циркониевого сплава – 0,85.

При испытании кольцевого образца сначала происходит изгиб и охват образцом полуцилиндрических опор с последующим образованием прямолинейных участков между опорами. В момент изгиба возникают участки локализации деформации, которые характеризуются коэффициентом деформации k. Коэффициент k позволяет учитывать проскальзывание кольцевого образца по поверхности захватов и вносить поправку при выборе начальной расчетной длины рабочей части образца l0 (рис. 2).

 

Величина локализованной деформации определяется на участках деформации образца на опорах l з’ и l з’’ (см. рис. 2). Коэффициент деформации k вычисляют по формуле [9–11]:

(3)  где lз’ и lз’’ – длина участков деформации образца на опорах, мм.

 

2. Аналитический способ определения коэффициента деформации k

2.1. Построение математической модели 

Для построения математической модели напряженно-деформированного состояния рассмотрим бесконечно малый элемент дуги dS = r*dx (рис. 3), находящийся в равновесии под действием внешних (qy, qz) и внутренних сил (Qy, Nz – поперечная и продольная силы, Mx – изгибающий момент) [12–14].

Составим для выбранного элемента три уравнения равновесия: суммы проекций всех сил на оси Z, Y и суммы моментов относительно оси X в точке без учета моментов от qy, qz, как бесконечно малых второго порядка малости:

Рис. 3. Бесконечно малый элемент дуги

С учетом бесконечного малого угла d x, будем считать, что cosdx  1, sindx  dx, dQy*dx  0, dNz*dx  0. Тогда система (4) принимает вид:

 

Для получения полной математической модели деформированного состояния кругового стержня рассмотрим геометрическое и физические соотношения. При этом будем пренебрегать изменением длины дуги dS до и после нагружения, а учитывать лишь перемещения сечений вдоль осей Y, Z соответственно Vy, Wz и относительный угол поворота сечений x (рис. 4).

 

Заменив малые дуги dS их длинами, спроецируем замкнутую ломаную ABCDEF на оси соответственно:

Отбрасывая бесконечно малые величины второго порядка малости, с учетом того, что cosdx  1, sindx  dx и cosx  1, sinx  dx приводим систему (6) к следующему виду:

 

Для дальнейших рассуждений воспользуемся известным выражением для изменения кривизны стержня, нагруженного изгибающим моментом:

(8) где Е – модуль упругости, Н/мм2;

J – момент инерции сечения, мм4.

Кривизна, в общем случае определяется выражением:

Значит , приращение будет определяться формулой:

Таким образом, с учетом (8) и (10), физическое соотношение, основанное на законе Гука с учетом жесткости сечения, необходимое для вычисления угла поворота сечения, имеет вид:

 

Полная математическая модель кругового стержня постоянной кривизны, нагруженного внешними силами постоянной интенсивности, может быть представлена системой:

 

С учетом больших перемещений система (6) имеет вид:

 

При бесконечно малом шаге интегрирования dx и принятых величинах второго порядка малости cosdx  1, sindx  dx и dVy*sindx  0, получим систему (14) или конечно-разностном виде – систему (15).

 

Решение системы уравнений (12) определяет внутренние силы, перемещения (Vy, Wz – радиальное и продольное перемещения) и угол поворота сечения x во всем диапазоне текущего угла x. Для решения системы (12) воспользуемся представлением производной функции f в точке i (i = 0…n) в виде:

где dx = 2/n – шаг приращения текущего угла x, который должен быть достаточно мал, что, например, достигается при n  360 для замкнутого стержня.

При таком подходе система (12) может быть представлена в виде:

Для решения системы (17) можно использовать стандартную процедуру «Поиск решения», интегрированную в табличный процессор MS Excel, определив начальные параметры Nz0, Qy0, Mx0, Wz0, Vy0, x0 путем их варьирования при соблюдении набора граничных условий [9–13].

2.2 Авторский шаблон для аналитического решения инженерных задач 

Авторский шаблон для аналитического решения инженерных задач представляет собой электронный файл, разработанный в общедоступном табличном процессоре MS Excel [12–16]. Шаблон содержит электронные таблицы и графики, позволяющие проводить анализ напряженно-деформированного состояния исследуемого объекта.

Рабочая область электронной таблицы шаблона разбита на следующие сектора: 1 – исходные данные, 2 – расчетная схема, 3 – таблица расчетов, 4 – график деформированного состояния; также для проведения расчета коэффициента заторможенности k добавлены сектора: 5 – геометрия, 6 – таблица расчета периметра и 7 – график распределения суммарного перемещения U по полупериметру кольца Р (рис. 5).

2.3 Постановка задачи и решение

Требуется вычислить коэффициент деформации k (3) при растяжении кольцевого образца с геометрическими и физическими характеристиками: D – наружный диаметр, мм; а – толщина стенки, мм; b – ширина образца, мм; Dз – диаметр опор захвата, мм; E – модуль упругости материала при конкретной температуре, Н/мм2.

Решение задачи сводится к определению значений длин участков деформации  lз’ и lз’’ кольцевого образца при изгибе на полуцилиндрических опорах (см. рис. 2).

Для решения данной задачи в сектор 1 (рис. 5) задавали модуль упругости материала E, а в сектор 5 – геометрию конкретного образца. Распределенную нагрузку qy задавали по периметру кольца, ограниченному на двух участках углом , который вычисляли по формуле (сектор 2 на рис. 5):

(18)  где lз – длина дуги полуцилиндрической опоры захвата с учетом скосов, мм;

Dср – средний диаметр кольца, мм.

Далее для подбора начальных параметров Nz0, Qy0, Mx0, при граничных условиях x0 = Vy0 = Wz0 = 0, подбирали значение нагрузки q y и запускали стандартную процедуру «Поиск решения» до тех пор, пока не выполнится условие равенства:

(19)  где |y0| + y180 – длина участка деформированного кольца между координатами точек y0 и y180 при AL = 0 и AL = 180, мм;

Dз + a – расстояние среднего диаметра кольца, деформированного на опоре, мм

Рис. 5. Общий вид шаблона для аналитического решения

 

Например, для кольцевых образцов D = 6,9 мм и а = 0,4 мм, изготовленных из оболочечных труб, применяемых в качестве тепловыделяющих элементов реактора БН-600, при использовании опор Dз = 4,8 мм, равенство (19) составляет 5,2 мм.

После выполнения подбора необходимого значения q y строили график распределения суммарного перемещения U по полупериметру кольца Р от точки z90 до z270 при AL = 90 и AL = 270 (сектор 7 на рис. 5). Суммарное перемещение вычисляли по формуле:

 

График распределения U по P отражает деформацию кольца с учетом системы (15). Точки z ’ и z’’ обозначают месторасположение торца полуцилиндрических опор, где заканчивается ввод значений распределенной нагрузки qy.

На графике (сектор 7 на рис. 5) видно, каким образом происходит локализация деформации кольца с учетом геометрии опоры. Для вычисления коэффициента деформации k по графике распределения U по P с помощью математической обработки вычисляли точки пересечения касательных, приведенных к кривой, и определяли значения l’ и l’’. Далее вычисляли k по формуле (3).

 

3. Анализ результатов

3.1. Влияние параметров образца на величину коэффициента k

Чтобы оценить аналитический способ определения коэффициента k с помощью авторского шаблона проводили расчет для небольшой выборки кольцевых образцов, изготовленных из тонкостенной оболочечной трубы наружным диаметром D = 6,9 мм, толщиной стенки a = 0,4 мм ( 6,90,4), ширина образцов b варьировалась от 2,25 до 2,58 мм, материал – аустенитная сталь ЧС-68. Испытание на растяжение проводили на полуцилиндрических опорах диаметром D з = 4,8 мм при комнатной температуре (20°С), а так же в низкотемпературном (400 и 450 °С), среднетемпературном (500 и 550 °С), высокотемпературном (600 и 650 °С) диапазонах, согласно методике [3].

В качестве физического параметра использовали модуль упругости E стали  ЧС-68, определенный динамическим резонансным методом в перечисленных диапазонах [23].

В таблице 1 представлены результаты расчета коэффициента k при заданных геометрических и физических параметрах кольцевого образца. Среднее значение коэффициента k для исследуемой выборки образцов составляет 0,5550,003. Ограничиваясь двумя знаками после запятой, для исследуемой выборки среднее значение примем k  = 0,55.

Таблица 1

 

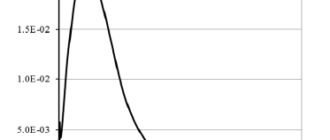
Для демонстрации влияния параметров образца на величину коэффициента k удобно воспользоваться построением зависимости от осевого момента сопротивления поперечного сечения образца Wx (рис. 6), который вычисляли по формуле:

Рис. 6. Зависимость коэффициента k от Wx

Из зависимости k от W x (рис. 6) можно сделать вывод, что более высокие значения коэффициента k, относительно среднего значения, наблюдаются у образцов, обладающих более податливым поперечным сечением, т.е. при меньших значениях Wx. Хаотичный разброс значений коэффициента k, полученных в результате анализа при различных температурах, указывает на то, что модуль упругости E оказывает меньшее влияние на величину коэффициента k, по сравнению с геометрическими параметрами.

3.2 Влияние коэффициента k на определение начальной расчетной длины образца l0

Согласно стандарту [4] начальную расчетную длину рабочей части образца на растяжение вычисляют по формуле:

где F0 – начальная площадь поперечного сечения образца, мм2.

Коэффициент деформации k позволяет вносить поправку определении длины l0 кольцевого образца, вычисляемой по формуле (2). Однако в работах [9–11] для сталей был принят коэффициент k = 0,5, полученный путем усреднения экспериментальных данных на кольцах различных типоразмеров. Это вносит ошибку, относительно стандартного значения (22), при выборе l0 для кольцевых образцов с отличающимися геометрическими параметрами поперечного сечения, а также при использовании полуцилиндрических опор разного диаметра. Коэффициент k, полученный аналитическим способом для каждого конкретного образца, позволяет уменьшить ошибку и разброс значений l0 исследуемой выборки (рис. 7). На рисунке показано, что использование аналитических значений коэффициента k уменьшает среднеквадратическое отклонение в 2,5 раза.

Рис. 7. Разброс значений l0 исследуемой выборки

 

Для кольцевых образцов 6,90,4, исследуемых по методике [3], F0  1 мм2, тогда l0 можно принять равным 5,65 мм. В таблице 2 приведено сравнение усредненных значений l 0, рассчитанных по формуле (2) с использованием экспериментального kэксп. = 0,5 и аналитического kанал. = 0,55, с выбранным стандартным значением (22). Видно, что рассчитанные значения отличаются между собой на  8 %, а значение l 0, рассчитанное с помощью аналитического kанал., приближается к стандартному.

Таблица 2

Сравнение средних расчетных значений l0 со стандартным

 

3.3 Коэффициент деформации k кольцевых образов различных типоразмеров

В таблице 3 приведены результаты аналитического расчета коэффициента деформации k для кольцевых образцов различных типоразмеров, а также сравнение значений начальных расчетных длин рабочей части l0, вычисленных по формулам (2) и (22). Модуль упругости E аустенитной стали ЭИ-844БУ в исходном состоянии определяли по результатам измерений согласно методике [23] при комнатной температуре 20 °С, а модули труб из циркониевого сплава Э-110 и сплава ниобия (в отожженном состоянии) принимали согласно справочным данным [24].

Таблица 3

Коэффициент деформации k для кольцевых образцов различных типоразмеров

 

Можно сделать вывод, что коэффициент деформации k, полученный аналитическим способом, улучшает результаты определения начальной расчетной длины рабочей части l 0 кольцевого образца относительно стандартного значения, вычисленного по формуле (22). Полученные результаты отличаются между собой не более чем на 11 % для труб из циркониевого сплава Э-110 и не более чем на 21 % для аустенитной стали ЭИ-844БУ.

Для оболочечной трубы из ниобия коэффициент деформации k = 0,62, а разница между начальными расчетными длинами рабочей части, вычисленных по формулам (2) и (22), не превышает 5 %.

 

Заключение

Описанный аналитический способ позволяет определять коэффициент деформации k кольцевых образцов различных типоразмеров и, тем самым, вычислить начальную расчетную длину рабочей части образца, приближенную к стандартному значению, полученному по формуле (22).

Для объективного анализа коэффициента деформации k новых материалов оболочечных труб требуется проведение большого объема экспериментов, подобных работам [9–11].

 

Список литературы

1. ОИ 001.325-2006. Методика выполнения испытаний для определения характеристик механических свойств при растяжении образцов труб в поперечном направлении из сплавов циркония. – АО «ВНИИНМ», 2006. – 30 с.
2. СТП 086-288-99. Оболочки облученных и необлученных твэлов. Методика выполнения измерений характеристик механических свойств при растяжении кольцевых образцов из тонкостенных труб из стали и сплавов. – ГНЦ РФ «НИИАР», 1999. – 18 с.
3. МК 10.13/03. Определение характеристик механических свойств при растяжении образцов продукции из конструкционных материалов. – АО «ИРМ», 2017. – 24 с.
4. ГОСТ 1497-84. Металлы. Методы испытаний на растяжение. – Москва, 2006. – 24 с.
5. Chris P. Dick, Yannis P. Korkolis. Mechanics and full-field deformation study of the Ring Hoop Tension Test // International Journal of Solids and Structures. – 2014. – 51 – P. 3042-3057.
6. Andreiev A., Golovko O., Frolov I., Nürnberger F., Oliver L., Schaper M., Grydin O. Testing of pipe sections // Component-oriented testing. – 2015. – 57 (2015) 7-8 – P. 643648.
7. Ожигов Л.С., Митрофанов А.С., Савченко В.И., Вьюгов П.Н., Крайнюк Е.А. Определение пластичности металлических труб малых диаметров в тангенциальном направлении // Заводская лаборатория. Диагностика материалов. – Т. 80, № 3. – 2014. – С. 60 – 62.
8. Костюхина А.В. Расчетно – экспериментальное исследование механических свойств и деформационного поведения материалов оболочек твэлов энергетических реакторов в тангенсальном направлении: Автореферат диссертации на соискание ученой степени кандидата технических наук. – М.: НИЯУ МИФИ, 2017. – 26 с.
9. Отчет п/я Р-6575. «Метод определения относительной пластической деформации кольцевых образцов малых диаметров по диаграмме растяжения». – 1976. – 18 с.
10. Отчет п/я A-1758 и п/я Р-6575. «Некоторые методические вопросы определения кратковременных механических свойств твэльных труб из сплава 110 в поперечном направлении». – 1976. – 36 с.
11. Отчет п/я A-1758 и п/я Р-6575. «Методика определения кратковременных механических свойств твэльных труб из стали ЭИ-844БУ на кольцевых образцах». – 1979. – 27 с.
12. Соколовский З.Н., Макеев С.А., Степанова Е.П. Численное решение задачи плоского изгиба и растяжения (сжатия) прямых стержней без ограничения величины перемещений // Омский научный вестник. – 2005. – № 4(33) – С. 120–123.
13. Макеев С.А., Краснощеков Ю.В., Соколовский З.Н. Инженерная методика анализа пространственного деформирования упругих прямых стержней с учетом геометрической нелинейности // Известия вузов. Строительство. – 2017. – № 11–12 – С. 81–91.
14. Гришаев Н.А., Белый В.Д., Макеев С.А. Аналитическое решение плоской задачи для кругового стержня. // Материалы IV научно-практической конференции студентов, аспирантов и молодых ученых 20–21 мая 2009 г. – Омск: изд-во СибАДИ, 2009. Кн. 3 – С.62–68
15. Соколовский З.Н., Макеев С.А. Электронный учебно-методический комплекс по курсу «Сопротивление материалов», «Статика и динамика плоских стержневых систем»// Омский научный вестник. – 2005. – № 3(32) – С. 211–214.
16. Соколовский З.Н., Макеев С.А. Электронный учебно-методический комплекс «Статика и динамика плоских стержневых систем» по курсу «Сопротивление материалов»// Электронный научный журнал «Вестник Омского государственного педагогического университета. – 2006. www.omsk.edu
17. Макеев С.А., Кузьмин Д.А., Гришаев Н.А. Способ определения остаточных напряжений / Патент RU 2455622 C1, заявка 2011105715/28 от 15.02.2011. – М.: Роспатент, 2012.
18. Писаренко Г.С., Агарев В.А., Квитка А.Л., Попков В.Г., Уманский Э.С. Сопротивление материалов: Учебник для вузов / Под ред. акад. АН УССР Г.С. Писаренко – 4-е изд., испр. и доп. – Киев: Высшая школа. Головное изд-во, 1979. – 696 с.
19. Варданян Г.С., Андреев В.И., Атаров Н.М., Горшков А.А. Сопротивление материалов с основами теории упругости и пластичности: Учебник / Под ред. Г.С. Варданяна и Н.М. Атарова. – 2-е изд., испр. и доп. – М.: ИНФРА-М, 2014. – 512 с.
20. Сен-Венан Б. Мемуар о кручении призм / Под ред. Г.Ю. Джанелидзе. – М.: Физматгиз, 1961. – 518 с.
21. Эйлер Л. Метод нахождения кривых линий, обладающих свойством максимума либо минимума. – М.–Л.: ГТТИ, 1934. – 601 с.
22. Красотина Л.В. Выбор параметров сборных профилированных несущих оболочек по критериям прочности и жесткости: Автореферат диссертации на соискание ученой степени кандидата технических наук. – Омск: СибАДИ, 2014. – 23 с.
23. МК 10.3/03. Методика измерений характеристик упругости динамическим резонансным методом. – АО «ИРМ», 2017. – 26 с.
24. Физические свойства сталей и сплавов, применяемых в энергетике, справочник / Под редакцией канд. техн. наук Б.Е. Неймарк – М. – Л.: Изд. «Энергия», 1967. – 240 с.