Расчетный анализ экспериментальных данных по теплообмену в пучках стержней, охлаждаемых водой сверхкритического давления

Деев В.И., Баисов А.М. (НИЯУ «МИФИ», Москва, Россия)

Введение

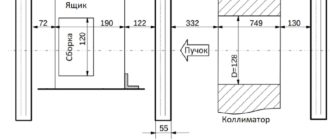
Ядерные реакторы со сверхкритическими параметрами воды утверждены Международным форумом «Генерация – IV» (GIF) в качестве перспективных ЯЭУ 4-го поколения. Как показывают оценки, создание таких реакторов обеспечит значительный рост коэффициента полезного действия АЭС, приведет к возможности использования одноконтурной схемы, позволяющей уменьшить количество единиц оборудования и габариты станции, а тем самым существенно сократить стоимость и сроки строительства. За счет высокой теплоемкости воды при сверхкритическом давлении удается значительно снизить расход теплоносителя и уменьшить затраты на его прокачку через активную зону по сравнению с традиционными легководными ректорами. Таким образом, экономика атомной станции и ее экологическая безопасность будут значительно выше [1].

Одна из основных проблем создания реакторов с водой сверхкритического давления – надежное описание теплообмена в активной зоне. В условиях заданной плотности теплового потока недопустимость превышения предельного перегрева оболочек тепловыделяющих элементов, что непосредственно связано с коэффициентом теплоотдачи, становится главным критерием при оценке целостности первого барьера безопасности реактора. Сложность проблемы заключается в том, что при сверхкритическом давлении физические свойства воды резко изменяются с температурой. Это практически исключает возможность использования для расчета конвективной теплоотдачи соотношений, справедливых для теплоносителей с постоянными свойствами. Вследствие трудностей теоретического анализа для получения новых расчетных зависимостей в данном случае используют эмпирические методы, основанные на обобщении результатов экспериментальных работ.

1. Экспериментальные работы и анализ полученных данных

До 2008 года была известна только одна экспериментальная работа, проведенная в СССР во Всесоюзном теплотехническом институте, в которой исследовался теплообмен при движении воды сверхкритического давления в семистержневом пучке со спиральными ребрами [2]. В настоящее время полученные в этой работе данные считаются утерянными. Несколько позднее появились сообщения о проведении в Киевском политехническом институте исследований теплоотдачи к потоку воды СКД в узких кольцевых каналах, трех- и семистержневых пучках. Однако представленные в докладах [3–5] украинских специалистов опытные данные для пучков слишком малочисленны и поэтому далее не рассматриваются.

Наиболее представительные эксперименты по теплоотдаче при турбулентном течении воды сверхкритических параметров в вертикально расположенных пучках стержней выполнены в Китайской Народной Республике. В Сианьском университете (Xi’an Jiaotong University) группа исследователей лаборатории многофазных течений сконструировала экспериментальный контур для измерения коэффициента теплоотдачи к воде сверхкритического давления в вертикальных каналах. В 2014 году были опубликованы [6] результаты измерений, проведенных в квадратном пучке, состоящем из четырех обогреваемых электрическим током труб (пучок стержней 2×2). Уже в следующем году на Международном симпозиуме ISSCWR-7 были представлены [7], а в 2016 году опубликованы [8] результаты экспериментов с таким же пучком, но в котором на стержни была навита спираль из проволоки диаметром 1,2 мм (шаг спирали 200 мм).

В 2010 году Китайская ядерная энергетическая корпорация Гуандун (CGNPC) совместно с Шанхайским университетом (SJTU) завершила строительство исследовательского контура SWAMUP (Supercritical WAter MultiPurpose test loop) для изучения теплоотдачи к воде сверхкритического давления в трубах, кольцевых каналах и пучках стержней. На Международном симпозиуме ISSCWR-7 в 2015 году были доложены результаты измерений коэффициента теплоотдачи к воде в гладком пучке 2×2, эти же данные более подробно представлены в международных журналах [9, 10].

В последующие три года в серии статей [11, 12] и трудах Международного симпозиума ISSCWR-8, состоявшегося в 2016 году в Китае, приведены данные о теплоотдаче при подъемном и опускном течении воды СКД в пучке со спиральной навивкой из проволоки диаметром 1.65 мм (шаг навивки 250 мм).

Основные характеристики экспериментальных участков и диапазоны варьируемых параметров в опытах с пучками стержней приведены в таблице 1.

Таблица 1

Общая характеристика экспериментов с пучками стержней, охлаждаемых водой СКД

Примечание. * В колонке «Пучок» указан тип пучка. Условное наименование типа пучка 22 означает: пучок с четырьмя стержнями (нагреваемыми электрическим током трубами) диаметром d и длиной L, расположенными в квадратной решетке с относительным шагом s/d;  22 н.пр – то же самое для пучка со стержнями, на поверхность которых навита спираль из проволоки. В этой же колонке указано количество серий экспериментов, обработанных авторами доклада.

В целом анализ результатов представленных здесь экспериментов показывает, что основные закономерности конвективной теплоотдачи к воде сверхкритического давления в пучках стержней аналогичны наблюдавшимся ранее при движении воды СКД в круглых трубах. Вместе с тем следует отметить и некоторые особенности этого процесса. Геометрические неоднородности по сечению пучка приводят к неодинаковому распределению расходов и энтальпии теплоносителя в центральной и периферийных ячейках, что в свою очередь вызывает неоднородности в распределениях теплоотдачи и температуры стенки.

По данным измерений минимальная теплоотдача наблюдалась в периферийных (угловых) ячейках пучка с большим по отношению к центральной ячейке гидравлическим сопротивлением [13]. В соответствии с этим максимальная разность температур по окружности нагреваемой трубки достигала 10–15 °C. Представленные в работах [6–9, 12] данные о коэффициентах теплоотдачи в пучках рассчитаны по средним вдоль окружности стержня значениям температуры стенки. Анализ этих данных далее будем проводить на основе критериев и универсальных расчетных зависимостей для теплоотдачи к теплоносителям при сверхкритическом давлении, изложенных в наших работах  [14–16].

Согласно предложенной авторами доклада методике коэффициент теплоотдачи при нормальных режимах теплообмена в воде СКД может быть рассчитан по формуле

В случае каналов некруглого поперечного сечения в качестве определяющего размера в критериях Нуссельта и Рейнольдса используется гидравлический диаметр dг. Температура стенки tw, необходимая для определения значений плотности ρw и среднеинтегральной теплоемкости p с находится путем решения нелинейного уравнения /( Nu ) 0г b bw b t t qd    методом итераций.

Для учета изменения коэффициента теплоотдачи в режимах улучшенного или ухудшенного теплообмена в формулу (1) вводится дополнительный поправочный множитель Y, который является функцией двух безразмерных комплексов Am K ~ и h K ~ , включающих критерий Рейнольдса Rem, безразмерный тепловой поток /( ) pmmqm K q Gc   и безразмерный энтальпийный фактор m m h h h ( )/  в виде следующей комбинации:

В представленных здесь выражениях индекс m означает, что данная величина выбирается при псевдокритической температуре tm. Поправка (2) к формуле (1) не зависит от tw, поэтому коэффициент теплоотдачи можно определить из формулы

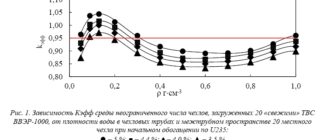
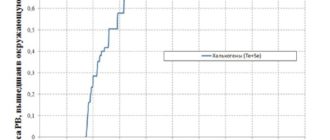
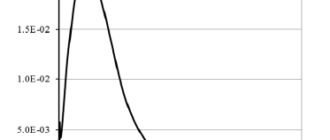
Совокупность экспериментальных данных [6–9, 12], обработанных по нашей методике, в целом составила 1815 опытных точек, полученных в 48 сериях экспериментов. На рисунке 1 приведены два примера такой обработки в виде зависимости отношения числа Нуссельта b эd  /Nu гэ  , найденного по экспериментальным данным, к числу Нуссельта, рассчитанному по формуле (1), от h K ~ при двух фиксированных значениях критерия

Рис. 1. Режимы улучшенной (а) и ухудшенной (б) теплоотдачи в пучках стержней

Результаты, представленные на рис. 1, позволяют сделать следующие выводы. Так же как и при течении внутри нагреваемых вертикальных труб, при наружном обтекании водой СКД пучков тепловыделяющих стержней наряду с нормальными режимами могут существовать режимы как улучшенной ( а), так и ухудшенной ( б) теплоотдачи. Последние два режима наблюдаются в псевдокритической области параметров в диапазоне -0.2 / K /-0.2  , при этом важную роль в реализации того или иного режима в относительно узких каналах играет комбинация критериев Рейнольдса 

ухудшенной. Более детальный анализ графических зависимостей, представленных на рисунке 1, позволяет заключить, что присутствие проволочной спирали на поверхности стержней лишь на несколько (около 10) процентов увеличивает коэффициент теплоотдачи, но совсем не исключает возможность ухудшения последней в псевдокритической области параметров при значениях 1 ~  AmK . То же самое можно сказать и в отношении влияния на теплоотдачу изменения направления потока в пучке.

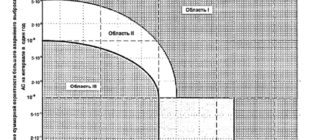
Расчетная методика, включающая уравнения (1) – (3), универсальна и может быть использована для определения коэффициента теплоотдачи во всех отмеченных выше режимах теплообмена при турбулентном течении воды сверхкритического давления в каналах разной конфигурации. Представление о качестве описания характеристик теплообмена в пучках тепловыделяющих стержней дает рисунок 2, где приведены все обработанные нами экспериментальные данные из работ [6–9, 12].

Рис. 2. Результаты обработки опытных данных по теплоотдаче в пучках стержней

Из рисунка 2 видно, что разброс экспериментальных значений числа Нуссельта Nuэ около расчетных Nuр практически не превышает  20 % за исключением отклонения небольшого количества точек, полученных в работе [12] для пучка с проволочной навивкой при энтальпии потока вблизи значения hm, соответствующего псевдокритической температуре tm. Это отклонение может быть связано частично как с интенсификацией теплообмена при закрутке потока, так и с погрешностями измерений, которые могут быть особенно велики при температурах, близких к tm. Статистический анализ отклонений расчетных и экспериментальных данных приведен в следующем параграфе.

2. Статистика результатов расчетов и сравнение с другими корреляциями

В процессе статистической обработки расчетных и экспериментальных данных вычислялись следующие величины:

– относительное отклонение найденного в экспериментах значения числа Нуссельта от расчетного для каждой опытной точки в виде k = (Nuэ/Nuр)k = (αэ/αр)k;

– среднеарифметическое σа, стандартное σст и среднеквадратичное σкв отклонения для совокупности значений k;

– относительная доля ( в %) опытных точек, отклоняющихся от кривой, рассчитанной по формулам (1)–(3), не более чем на 30 % – n30, соответственно на 20 % – n20, на 15 % – n15.

Для совокупности N опытных точек значения σа, σст и σкв определялись по формулам:

Результаты расчетов приведены в таблице 2. Из таблицы 2 следует, что система уравнений (1)–(3) удовлетворительно описывает данные по теплоотдаче, полученные в экспериментах со всеми пучками, при этом более чем 80 % из 1815 опытных точек расходится с результатами расчета менее чем на 20 %, а среднеквадратичное отклонение для всех изученных режимов теплообмена в воде составляет всего лишь 18,5 %. По понятным причинам наиболее высокие значения отклонений наблюдаются в области ПКС, здесь свойства воды изменяются особенно сильно и возможно возникновение разного типа неустойчивостей, приводящих к нестабильности теплообмена.

Наилучшее согласование данных расчета с экспериментальными значениями коэффициента теплоотдачи получено при описании опытов с гладкими пучками (при сравнении с опытными данными Gu et al., 2015 σкв = 0,13). В случае пучков стержней с навитой на них проволокой (пучки типа 2 2 н.пр) расчет по формулам (1)–(3) дает значения коэффициента теплоотдачи, которые занижены на 6–10 % по сравнению с опытными данными. Это неудивительно, так как закрутка потока вызывает эффект интенсификации теплообмена, который не учитывается формулой (1). Например, согласно [17] в закрученном потоке воды улучшение теплоотдачи может достигать 20 % по сравнению с тем, что дает расчет по формуле Диттуса–Болтера.

Таблица 2

Отклонения расчетов по формулам (1)–(3) от данных экспериментов с пучками 2х2

Для сравнения разработанной авторами методики расчета теплоотдачи к теплоносителям в области сверхкритических давлений было отобрано 10 других известных корреляций. При этом авторы руководствовались следующими принципами. Предпочтение отдавалось 1) формулам, которые получили широкое распространение и хорошо себя зарекомендовали при сравнении с опытными данными по теплообмену в круглых трубах; 2) соотношениям, специально разработанным с целью описания режимов ухудшенного теплообмена; 3) корреляциям, полученным на основе использования опытных данных для пучков стержней. Сводка отобранных таким образом уравнений приведена в таблице 3.

Относительно формул, представленных в таблице 3, можно сказать следующее. В публикациях, посвященных проблеме теплообмена в сверхкритической области параметров, традиционно отмечаются уравнения (4) и (5), а в последнее время часто цитируются и формулы (7)–(9). Уравнения (6), (7), (10), (11) претендуют на описание режимов ухудшенного теплообмена. Первые три из этих уравнений содержат безразмерный комплекс A, который в работе [21] назван критерием термического ускорения, а в последние два в той или иной модификации входит число Грасгофа Gr, с помощью которого принято описывать влияние на теплоотдачу архимедовых сил, или сил плавучести в движущемся потоке жидкости. Формула (12) получена авторами [6] в результате обобщения собственных измерений теплоотдачи в гладком пучке стержней 2×2.

За исключением формулы (7) все остальные уравнения содержат параметры, которые в неявном виде зависят от температуры стенки. Метод учета влияния на теплоотдачу переменности физических свойств теплоносителя в неизотермическом потоке с помощью так называемых параметрических факторов в виде отношения этих свойств при температуре стенки и среднемассовой температуре жидкости хорошо известен и уже давно используется в теплопередаче. Однако когда температура стенки заранее не известна, в процессе определения коэффициента теплоотдачи требуется проведение итерационных расчетов. Практика решения сложных нелинейных уравнений, подобных некоторым из представленных в таблице 3, показывает, что не всегда удается получить желаемые результаты [27, 28].

Таблица 3

Уравнения для расчета коэффициента теплоотдачи к воде сверхкритического давления

В наших расчетах, которые на первом этапе проводились с использованием базы данных по теплоотдаче в гладких пучках стержней, установлено, что применение метода итераций к уравнениям (10)–(12) во многих случаях дает неоднозначные результаты, а в некоторых областях режимных параметров, в которых проводились опыты [6–9, 12], решения уравнений (11) и (12) вообще отсутствуют. Статистические показатели, которые с количественной стороны характеризуют возможность описания различных режимов теплоотдачи к воде СКД в гладких пучках стержней, приведены в таблице 4.

В связи с явно неудовлетворительным описанием опытных данных формулы (9)– (13) далее не рассматриваются. (Соотношение Мокри и др. (8) оставлено лишь как пример формул, получивших широкое распространение, но не пригодных для расчета теплообмена в пучках стержней).

В таблице 5 представлены отклонения опытных данных для пучков с навитой на стержни проволокой от значений коэффициента теплоотдачи, рассчитанных по формулам (4)–(8), а в таблице 6 – результаты статистической обработки в целом всех данных, полученных в 48 сериях экспериментов [6–9, 12].

Таблица 4

Отклонения опытных данных для гладких пучков от расчета по формулам (4)–(13)

Примечания. * В 78 случаях решение отсутствует. ** В 284 случаях решение отсутствует.  *** Представлены результаты обработки данных только из 6 серий экспериментов.

Таблица 5

Отклонения данных для пучков с проволочной навивкой от расчета по формулам (4)–(8)

Представленные в последних трех таблицах статистические показатели позволяют сделать следующие выводы. Результаты проверки нескольких известных соотношений для труб на базе опытных данных по теплоотдаче к воде СКД в пучках обогреваемых стержней показывают, что пока только формулы (4)–(6) выдерживают испытания. Полученные при использовании этих формул отклонения расчетов от экспериментов в среднем лежат на уровне 20 % и соответствуют погрешности определения коэффициента теплоотдачи по нашей методике (см. таблицу 2). Такая погрешность приемлема в инженерной практике и маловероятно, что вследствие чрезвычайной сложности рассматриваемого явления она будет существенно снижена.

Заключение

Выполнено сопоставление опытных данных по теплообмену при движении воды сверхкритического давления в пучках стержней с результатами расчета коэффициента теплоотдачи по методике, предложенной авторами доклада, и некоторым другим соотношениям, разработанным ранее для круглых труб. Показано, что наилучшее согласование с экспериментом дают расчеты по методике Деева и др., а также уравнениям Бишопа с соавторами, Джексона–Фьюстера, Курганова–Анкудинова. Уровень погрешности таких расчетов около 20 %, что дает основание рекомендовать указанные корреляции для их использования в инженерных расчетах теплогидравлики активных зон реакторов с водой сверхкритического давления.

По сравнению с другими соотношениями преимущество методики Деева и др. заключается в ее универсальности. Используемые в этой методике критерии и специально построенная система уравнений позволяют проводить расчеты в режимах нормального, улучшенного и ухудшенного теплообмена в средах с сильно изменяющимися свойствами, при этом обеспечиваются непрерывные предельные переходы к состояниям, в которых свойства мало изменяются. В данной методике не возникает проблем при проведении итерационных расчетов, так как область, где возникает неоднозначность при решении нелинейного уравнения теплоотдачи, выведена за пределы зоны рабочих параметров, при которых используется теплообменная среда. Показано также, что данная методика успешно работает в случае ее применения к другим флюидам со сверхкритическими параметрами.

Список литературы

1. GIF (Generation IV International Forum), Technology Roadmap Update for Generation IV Nuclear Energy Systems – January 2014, OECD Nuclear Energy Agency, 2014.
2. Дядякин Б.В., Попов А.С. Теплоотдача и гидравлическое сопротивление тесного семистержневого пучка, охлаждаемого потоком воды при закритических параметрах состояния // Труды ВТИ. 1977. Вып. 11. С. 244–253.
3. Heat transfer to supercritical water in vertical 7-rod bundle / V.G. Razumovskiy, E.N. Pis’menny, A.E. Koloskov et al. // 16 th International Conference on Nuclear Engineering (ICONE-16). Orlando, Florida, USA, May 11–15, 2008.
4. Heat transfer to supercritical water in vertical annular channel and 3-rod bundle / V.G. Razumovskiy, E.N. Pis’menny, A.E. Koloskov et al. // 17th International Conference on Nuclear Engineering (ICONE-17). Brussels, Belgium, July 12–16, 2009.
5. Heat transfer to water at supercritical parameters in vertical tubes, annular channels, 3-and 7-rod bundles / V.G. Razumovskiy, E.M. Mayevskiy, A.E. Koloskov et al. //  21st International Conference on Nuclear Engineering (ICONE-21). Chengdu, China,  July 29–August 2, 2013.
6. Experimental investigation of heat transfer from a 22 rod bundle to supercritical pressure water / H. Wang, Q.C. Bi, L. Wang et al. // Nuclear Engineering and Design. 2014. Vol. 275. P. 205–218.
7. Experiments of heat transfer to supercritical water in a 2×2 rod bundle with wire-wrapped spacers / H. Wang, Q. Bi, Z. Ni et al. // 7th International Symposium on Supercritical Water Cooled Reactors (ISSCWR-7). Helsinki, Finland, March 15–18, 2015. Paper 2060.
8. Wang H., Bi Q.C., Leung L.K.H. Heat transfer from a 22 wire-wrapped rod bundle to supercritical pressure water // International Journal of Heat and Mass Transfer. 2016. Vol. 97. P. 486–501.
9. Experimental studies on heat transfer to supercritical water in 2×2 rod bundle with two channels / H.Y. Gu, Z.X Hu, D. Liu et al. // Nuclear Engineering and Design. 2015. Vol. 291. P. 212–223.
10. Heat transfer to supercritical water in a 22 rod bundle / H.Y. Gu, H.B. Li, Z.X. Hu et al. // Annals of Nuclear Energy. 2015. Vol. 83. P. 114–124.
11. Experimental study on heat transfer to supercritical water in 22 rod bundle with wire wraps / H.Y. Gu, Z.X. Hu, D. Liu et al. // Experimental Thermal and Fluid Science. 2016. Vol. 70. P. 17–28.
12. Experimental study on heat transfer of supercritical water flowing upward and downward in 22 rod bundle with wrapped wire / Z.X. Hu, H.B. Li, J.Q. Tao et al. // Annals of Nuclear Energy. 2018. Vol. 111. P. 50–58.
13. Nonuniform heat transfer of supercritical water in a tight rod bundle – Assessment of correlations / H. Wang, Q. Bi, L. Wang, L.K.H. Leung // Annals of Nuclear Energy. 2017. Vol. 110. P. 570–583.
14. Анализ соотношений для расчета нормальной теплоотдачи к потоку воды сверхкритического давления в вертикальных трубах / В.И. Деев, В.И. Рачков, В.С. Харитонов, А.Н. Чуркин // Атомная энергия. 2015. Т. 119. Вып. 3. С. 138–144.
15. Режимы теплообмена при движении воды сверхкритических параметров в вертикальных каналах / В.И. Деев, В.С. Харитонов, А.Н. Чуркин, А.М. Баисов // Теплоэнергетика. 2017. № 11. С. 75–83.
16. Universal dependencies for the description of heat transfer regimes in turbulent flow of supercritical fluids in channels of various geometries / V.I. Deev, V.S. Kharitonov, A.M. Baisov, A.N. Churkin // The Journal of Supercritical Fluids. 2018. Vol. 135. P. 160–167.
17. Лопина Р.Ф., Берглес А.Е.. Теплоотдача и потери давления в искусственно закрученном однофазном потоке воды // Теплопередача. 1969. № 3. С. 158–168.
18. Bishop A.A., Sandberg R.G., Tong L.S. Forced convection heat transfer to water at nearcritical temperatures and supercritical pressures. Report WCAP-2056 Part IV, Westinghouse Electric Corporation, Atomic Power Division, Pittsburgh, Pennsylvania, USA, November 1964.
19. Jackson J.D. Fluid flow and heat transfer at supercritical pressure // 14th International Topical Meeting on Nuclear Reactor Thermal Hydraulics (NURETH 14). Toronto, Ontario, Canada, September 25–29, 20011. Paper 574.
20. Курганов В.А., Анкудинов В.Б. Расчет нормальной и ухудшенной теплоотдачи в трубах при турбулентном течении жидкостей в околокритической и газовой области состояний // Теплоэнергетика. 1985. № 6. С. 53–58.
21. Cheng X., Yang Y.H., Huang S.F. A simplified method for heat transfer prediction of supercritical fluids in circular tubes // Annals of Nuclear Energy. 2009. Vol. 36. P. 1120– 1128.
22. Development of supercritical water heat-transfer correlation for vertical bare tubes / S. Mokry, I. Pioro, A. Farah et al. // Nuclear Engineering and Design. 2011. Vol. 241. P. 1126–1136.
23. Gupta S., Mokry S., Pioro I. Developing a heat-transfer correlation for supercritical-water flowing in vertical tubes and its application in SCWR // 19th International Conference on Nuclear Engineering (ICONE-19). Osaka, Japan, October 24–25, 2011. Paper 43503.
24. Liu X., Kuang B. Wide-ranged heat transfer correlations of supercritical water in vertical upward channels // Chinese Journal of Nuclear Science and Engineering. 2012. Vol. 32 (4). P. 344–354 (in Chinese).
25. Chen W., Fang X. A new heat transfer correlation for supercritical water flowing in vertical tubes // International Journal of Heat and Mass Transfer. 2014. Vol. 78. P. 156–160.
26. Wang C., Li H. Evaluation of the heat transfer correlations for supercritical pressure water in vertical tubes // Heat Transfer Engineering. 2014. Vol. 35 (6–8). P. 685–692.
27. Чуркин А.Н., Деев В.И. Неоднозначность результатов расчета теплоотдачи к воде при использовании эмпирических корреляций в области сверхкритических давлений // ВАНТ. Серия: Обеспечение безопасности АЭС. 2012. Вып. 32. Реакторные установки. С. 65–75.
28. A new assessment method for the evaluation of supercritical heat transfer correlations, particularly with regard to the “multiple/no solutions” problem / T. Gschnaidtner, G.A. Schatte, A. Kohlhepp et al. // Thermal Science and Engineering Progress. 2018. Vol. 7. P. 267–278.