Удельные активные сопротивления проводов r0 , Ом/км, приводятся в справочниках. Для алюминиевых проводов произведение сечения провода F и его активного сопротивления r0 практически постоянно (определяется характеристиками алюминия). Некоторые отличия от среднего значения обусловлены конструкцией провода (числом и диаметром свитых проволок и наличием сердечника из стальных проводов в проводах марки АС).
Проводимость стали намного ниже алюминия, однако наличие дополнительного проводника несколько снижает общее сопротивление. Так, для проводов с сечением алюминия 185 мм2 и сечениями стального сердечника 29 и 43 мм2 удельные сопротивления составляют 0,159 и 0,156 Ом/км. Произведение F ⋅ r 0 для всех используемых марок проводов находится в диапазоне 27,2–30,4. В связи с этим в оценочных расчетах используют формулу r0 = 28,5 / F.
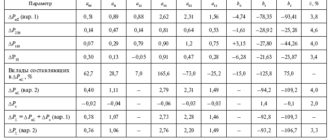
На некоторых старых ВЛ 0,4 кВ, а иногда и 6–10 кВ остались стальные провода марок ПСО-3,5; ПСО-4 и ПСО-5 (цифра означает диаметр провода в мм), а также ПС-25 (35, 50, 70; цифра означает сечение провода). Их активное сопротивление сильно зависит от протекающего тока. Например, для ПСО-5 при токе 1,5 А r0 = 7,9 Ом/км, а при токе 20 А r0 = 12,7 Ом/км. Для ПС-35 при тех же токах r0 = 5,26 и 6,7 Ом/км.
Активные сопротивления проводов ВЛ существенно зависят от температуры окружающего воздуха. Эта зависимость имеет вид (прил. 2):
Коэффициент kарм. принимают равным 1,02 для линий 110 кВ и выше и равным нулю для линий более низких напряжений (см. прил. 2). Наличие в формуле параметра j предусматривает учет некоторого превышения температуры провода над температурой окружающего воздуха за счет нагрева провода проходящим по нему током. Как следует из формулы (2.39), при плотности тока 1 А/мм2 нагрев провода сечением F = 300 мм2 повысит его температуру на 8,3 °С, что приведет к увеличению сопротивления на 3,3 %.
Для проводов меньших сечений влияние тока снижается (более тонкий провод охлаждается быстрее, так как тепловыделение в проводе пропорционально сечению, а площадь охлаждения – длине окружности). Например, для провода сечением F = 120 мм2 оно составит 5,2 °С. При отсутствии данных о средней плотности тока за расчетный период можно принять j = 0,5 А/мм2 . В этом случае приведенные значения повышения температуры провода снизятся в четыре раза.
Температура провода зависит не только от температуры окружающего воздуха и тока в проводе, но и от солнечной радиации, приводящей к некоторому его нагреву, и от силы и направления ветра, приводящего к охлаждению провода. Учет действительных значений солнечной радиации, силы и направления ветра в практических расчетах затруднен в силу информационной необеспеченности.
В связи с тем, что степень воздействия этих двух факторов на температуру провода значительно меньше, чем первых двух, а также учитывая противоположную направленность их воздействия, в практических расчетах ими можно пренебречь.
Реактивные (индуктивные) сопротивления проводов определяются внутренним и внешним магнитными полями. Характеристики внутреннего поля определяются материалом проводника, а внешнего – диаметром провода и его расположением относительно земли и особенно относительно проводов других фаз. Для алюминиевых проводов внутреннее реактивное сопротивление пренебрежимо мало.
Расположение проводов влияет на характеристики внешнего 53 магнитного поля слабее, чем диаметр провода, хотя и последний в силу логарифмической зависимости индуктивного сопротивления от геометрических размеров и сравнительно небольших различий в диаметрах проводов также не оказывает существенного влияния на величину сопротивления.
В частности, для проводов сечением 70 мм2 , подвешенных на опорах линий 35 и 110 кВ (геометрические размеры различны), удельные реактивные сопротивления x0 равны соответственно 0,432 и 0,444 Ом/км (различие – 2,8 %). Для провода сечением 240 мм2 на линии 110 кВ x0 = 0,405 Ом/км, что на 9,6 % ниже x0 = 0,444 Ом/км для провода сечением 70 мм2 . В оценочных расчетах часто используют значение x0 = 0,4 Ом/км.
Внутреннее реактивное сопротивление стальных проводов существенно, поэтому общее реактивное сопротивление определяют как сумму внешнего сопротивления, аналогичного сопротивлению алюминиевых проводов, и внутреннего, сильно зависящего от протекающего тока. Например, для провода ПСО-5 при токе 1,5 А внутреннее реактивное сопротивление x0в = 2,13 Ом/км, а при токе 20 А x0в = 10,5 Ом/км. Для ПС-35 при тех же токах x0в = 0,34 и 1,04 Ом/км. Поэтому при расчетах сетей со стальными проводами необходимо учитывать зависимости их активного и реактивного сопротивления от протекающего тока.
Кроме сопротивления проводов воздушные линии характеризуются емкостной проводимостью на землю. Хотя провод имеет сравнительно малые размеры, он вместе с землей представляет собой конденсатор, одна обкладка которого имеет потенциал фазного провода, а другая – ноль. Емкость такого конденсатора характеризуется удельной емкостной проводимостью b0 , См/км (Сименс на 1 км), приводимой в справочниках.
Генерируемую линией реактивную мощность определяют по формуле Qc = b0 U 2 . Несмотря на малые значения b0 , при большой протяженности линии значения Qc оказываются существенными. Особенно это характерно для линий 330–750 кВ в связи с применением на них расщепленной фазы, увеличивающей эквивалентный радиус провода и соответственно значение b0 . Реактивная мощность, генерируемая одним километром линий различного напряжения, составляет:

В расчетах режимов линию представляют в виде ∏-образной схемы с соответствующими продольными активным и реактивным сопротивлением и поперечными емкостными проводимостями по концам линии, каждая из которых равна половине суммарной емкостной проводимости.
Трансформаторы характеризуются активным и реактивным сопротивлениями и активными и реактивными потерями мощности холостого хода. Эти параметры приводятся в справочниках. Трехобмоточные трансформаторы (автотрансформаторы) в расчетных схемах представляют в виде звезды, реактивные сопротивления лучей которой определяют по данным о напряжениях короткого замыкания, а активные сопротивления – по потерям мощности короткого замыкания между каждой парой обмоток. Для большинства трансформаторов и автотрансформаторов потери мощности короткого замыкания приводятся в виде одной величины. Поэтому активные сопротивления лучей приходится принимать одинаковыми. Расчетные значения сопротивлений двухобмоточных трансформаторов и лучей трехобмоточных трансформаторов (автотрансформаторов) и сопротивлений проводов при температуре провода t п = 20 °С приведены в прил. 9.