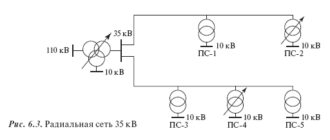
При расчете интегрирующих множителей обычным является допущение о чисто квадратичной зависимости нагрузочных потерь от нагрузки. При этом допущении интегрирующий множитель Мр для определения потерь электроэнергии по потерям мощности, рассчитанным для режима с нагрузкой Pр , определяют по формуле, ч:

Значение Мр выражается в тех же единицах, что и ∆Т, и физически представляет собой эквивалентную продолжительность режима с нагрузкой Pр , в течение которой потери мощности ∆Pр приведут к таким же потерям энергии, что и при ее потреблении по реальному графику. Если ∆Pр рассчитано для режима максимальной нагрузки, то Мр представляет собой число часов максимальных потерь t.
Если ∆Pр рассчитано при нагрузке меньше максимальной, то Мр будет больше числа часов максимальных потерь и в некоторых случаях оно может оказаться даже больше продолжительности расчетного периода Т. Эта ситуация может наблюдаться при расчете Мр для элемента сети, потери электроэнергии в котором относят не к его максимальной нагрузке, а к его нагрузке в режиме максимальной нагрузки сети в случае, когда эти два режима не совпадают во времени.
В силу того, что интегрирующие множители используют для расчета потерь за расчетные периоды различной продолжительности, запишем формулу (2.2) в относительных единицах:

Аналогичное выражение можно записать и для графика реактивной мощности. Абсолютное значение множителя определяют умножением относительной величины на продолжительность расчетного периода.
На практике в качестве расчетных режимов используют либо режим максимальной нагрузки сети Pмакс, определяемой по контрольным замерам, либо средней Pср, определяемой по показаниям счетчиков. В первом случае интегрирующий множитель представляет собой относительное число часов наибольших (максимальных) потерь:

Метод, использующий величину τ0 , называется методом наибольших потерь.
Во втором случае интегрирующий множитель является произведением Т на квадрат коэффициента формы графика нагрузки, определяемый по формуле

Метод, использующий величину 2 ф k , получил название метода средних нагрузок. Величины (2.4) и (2.5) связаны между собой соотношением

Значение τ0 для реальных графиков нагрузки меньше единицы, 2 ф k – больше единицы, и лишь для графика, выраженного прямой линией (узел с неизменной нагрузкой), τ0 = 2 ф k = 1. В расчетах потерь электроэнергии всегда используется значение квадрата коэффициента формы графика. Сам коэффициент формы графика обычно не определяют. Поэтому в дальнейшем для краткости используется термин «коэффициент формы графика», под которым понимается его квадрат.
Оба описанных метода технологически мало отличаются друг от друга; они исходят из расчета потерь мощности только в одном режиме: в первом случае – максимальных нагрузок, во втором – средних нагрузок. В дальнейшем эти методы называются, соответственно, метод 1 и метод 2.
Коэффициент заполнения графика нагрузки kз определяют по формуле

Значение kз определяется соответствующими этому периоду значениями энергии W и максимальной нагрузки Pмакс. В летние месяцы график может быть достаточно плотным и иметь значение kз выше, чем в зимние месяцы. Однако его влияние на kз.г. для годового периода будет даже меньше, чем для зимнего месяца kз.з., так как потребление в летние месяцы будет соотноситься с зимним максимумом нагрузки. Соотношение значений kз.г. и kз.з. отражается формулой kз.г. = kз.з. Wср /Wз , где Wср – среднемесячное потребление энергии, а Wз – потребление за зимний месяц. Потребление за зимний 36 месяц, как правило, больше среднегодового, поэтому для годового периода kз и τ0 меньше, а 2 ф k больше, чем для зимнего месяца.
Если значение τ0 рассчитано для суточного графика дня контрольных замеров, (обозначим его τс ), то его значение для года рассчитывают по формуле

Значение τN рассчитывают по формуле




Обычно график нагрузки представляется последовательностью почасовых значений. Если значения располагают в порядке их снижения, такой график называют графиком «по продолжительности нагрузок». При наличии данных об отношении минимальной и максимальной нагрузок kмин = Рмин /Рмакс могут быть использованы более точные (но тоже приближенные) формулы.
Они исходят из представления графика по продолжительности плавной убывающей функцией, которая в зависимости от соотношения kз и kмин может быть вогнутой или выпуклой. Характер функции определяют на основе предварительно рассчитанного параметра λ = (kз – kмин)/(1 – kз ). При λ < 1 функция вогнутая, при λ > 1 выпуклая, при λ = 1 она представляет собой прямую линию. Значения τ0 определяют по формулам [1]:

В прил. 1 показано, что диапазон возможных погрешностей формул (2.16) и (2.17) имеет практически нулевую систематическую погрешность. Диапазон случайной погрешности с вероятностью 0,95 составляет ±13 %. Формулы (2.19) – (2.22) имеют систематическую погрешность –5 % (то есть в среднем потери занижаются на 5 %) и размах случайной погрешности ±10,8 % относительно среднего значения.
Систематическую погрешность можно скомпенсировать введением поправочного коэффициента 1,05; в этом случае формулы (2.19) – (2.22) оказываются точнее формул (2.16) и (2.17) на 2,2 %. Вместе с тем получение достоверных сведений о kмин бывает затруднено, а различие случайных погрешностей приведенных формул не выглядит существенным. Можно считать, что любые формулы, определяющие τ0 и 2 ф k только через kз или через kз и kмин, имеют неустранимую погрешность порядка ±(11–13) %. Свести ее к нулю 39 можно только применением формул (2.4) и (2.5), использующих значения ординат реального графика нагрузки.
Суточные графики реверсивных перетоков обычно нестабильны и имеет различную конфигурацию в разные сутки. Поэтому для среднесуточного графика приходится принимать предположение о равномерном распределении нагрузки на интервале от максимального значения потока в одну сторону до его максимального значения в другую сторону. В этом случае график имеет треугольный вид, для которого kз = 0,5. Для такого графика в соответствии с формулами (2.16) и (2.17) τ0 = 1/3, а 2 ф k = 4/3.
Эффект от режимных МСП (РН, оптимизация режимов и т. п.), часто рассчитывают в виде снижения потерь мощности в режимах максимальной δPмакс и минимальной δPмин нагрузок. При наличии графика нагрузки снижение потерь мощности в каждом часовом интервале можно определить из условия пропорциональности эффекта режимного мероприятия нагрузке рассматриваемого часа. При отсутствии графика используют его представление в виде двух ступеней с относительными продолжительностями режимов t макс и t мин, определяемыми по формулам:

Из формулы (2.23) следует, что kз не может быть меньше kмин.
Погрешности описанных выше приближенных формул относятся к методическим погрешностям. Методические погрешности определения τ0 и 2 ф k одинаковы, так как эти величины функционально связаны формулой (2.6). Тем не менее метод расчета потерь электроэнергии по средним нагрузкам дает гораздо более точные результаты, чем метод наибольших потерь. Это объясняется тем, что информационные погрешности данных о средних нагрузках, определяемых на основании показаний счетчиков, гораздо меньше, чем погрешности максимальных нагрузок, определяемых при контрольных замерах, выполняемых эпизодически и не всегда попадающих в действительный максимум.
Дальнейшее уточнение расчетов возможно при использовании суточных графиков узловых нагрузок, получаемых в дни контрольных замеров, проводимых в один из рабочих дней июня и декабря. Графики узловых нагрузок в другие месяцы можно определить, приняв допущение о характере изменения нагрузки узла на каждой ступени графика от июньского P6 до декабрьского P12 значения. 40 При допущении о линейном характере изменения нагрузки ее значение на рассматриваемой ступени графика в n-й месяц определяют по формуле

При расчете значений Pn за январь–май (n = 1–5) знак перед вторым слагаемым меняют на минус. При допущении об изменении нагрузки узла пропорционально изменению суммарной нагрузки сети P ∑ формула имеет вид

в зависимости от того, нагрузка какого месяца принята за базу.
При расчете потерь электроэнергии за месяцы текущего года приходится использовать графики контрольных замеров прошедшего года. Для расчета потерь требуется только конфигурация графика, а не его абсолютные значения, поэтому если конфигурация графика достаточно стабильна в течение года, то применять формулы (2.25) или (2.26) нет необходимости.
По энергии, потребленной (генерированной) в узле за рассматриваемый месяц, и принятой конфигурации графика определяют среднесуточный график нагрузки каждого узла в именованных единицах. Далее проводят расчет потерь мощности в сети (расчет УР) на каждой ступени графика и определяют потери электроэнергии за средние сутки месяца. Потери за месяц определяют по формуле
2 Δ =Δ WW k W ср.сут. м ф м ср.сут. м.экв. Д Д, = Δ (2.27)
где 2 ф м k – коэффициент, учитывающий неодинаковость потребления энергии в различные сутки месяца (2.14); произведение Дм 2 ф м k представляет собой эквивалентное число дней (суток) в месяце Дм. экв., за которые потери электроэнергии, рассчитанные за средние сутки месяца, будут равны сумме потерь, рассчитанных за каждые сутки месяца по фактическим суточным графикам.
В этом методе, называемом методом расчетных суток (метод 3), объединяются преимущества метода средних нагрузок (точное значение средней нагрузки, полученное на основе показания счетчика) с учетом индивидуальных конфигураций суточных графиков узловых нагрузок. Это позволяет рассчитать потери более точно, чем методами 1 и 2, использующими параметры одного графика – суммарной нагрузки сети.
Если потери электроэнергии рассчитывают за период, включающий в себя N месяцев, на основе ∆Wср. сут., рассчитанных за сутки одного из месяцев, то эквивалентное число дней определяют по формуле