Несимметричные режимы обусловливаются тремя причинами:
- неодинаковыми нагрузками фаз элементов сети, вызываемыми работой ЭП с нестабильной нагрузкой фаз (например, дуговых сталеплавильных печей) и однофазных ЭП (особенно это заметно в сетях 0,4 кВ, хотя и в промышленности существуют однофазные ЭП достаточно большой мощности);
- неполнофазной работой линий, вызванной кратковременным отключением одной из фаз линии при коротких замыканиях или более долговременным отключением при пофазных ремонтах, наличием поперечных реакторов не во всех фазах линии и т. п.;
- неравенством фазных параметров линий. Небольшое отличие фазных параметров обусловлено различием расположения проводов на опоре. Для выравнивания фазных параметров на линиях большой длины и высоких напряжений (330–750 кВ) осуществляют транспозицию проводов (поочередное изменение расположения фаз). Несимметрия напряжений, обусловленная этой причиной, на порядок меньше первых двух.
Наиболее частой причиной несимметрии напряжений на практике является неравенство токовых нагрузок фаз. При этом различают два вида несимметрии: систематическую и вероятностную несимметрию. Характерной чертой систематической несимметрии является постоянная перегрузка одной из фаз; в этом случае производят выравнивание нагрузок фаз путем переключения части нагрузок с перегруженной на недогруженную фазу.
Вероятностная несимметрия характеризуется попеременной перегрузкой то одной, то другой фазы (перемежающаяся несимметрия). В сетях 0,4 кВ городов и сельских населенных пунктов несимметрия напряжений вызывается в основном тем, что к этим сетям подключаются бытовые ЭП, являющиеся преимущественно однофазными, а в сетях более высоких напряжений – наличием у потребителей мощных однофазных нагрузок и трехфазных, но с неодинаковым потреблением по фазам. К последним относятся, в частности, дуговые сталеплавильные печи. Ток, проходящий по дуге каждой фазы, определяется расстоянием между электродом и шихтой.
Обвалы шихты в период ее расплава не позволяют поддерживать одинаковые расстояния во всех фазах и их токи оказываются разными. Другим мощным источником несимметрии являются тяговые подстанции 275 U1A U1A а б U1C U1C U1B U2A U0A ϕ2 ϕ0 U2B U U0B 2C U0C U2C U0C UC U2B U1B U0A U0B UA UB железнодорожного транспорта, электрифицированного на переменном токе, так как электровозы являются однофазными электроприемниками.
Любую несимметричную систему трех напряжений можно разложить на три симметричные системы: прямой последовательности U1 , чередование фаз которой совпадает с чередованием фаз исходной системы, обратной последовательности U2 , чередование фаз которой противоположное, и нулевой последовательности U0 , все векторы которой направлены одинаково (рис. 8.2).
Система векторов междуфазных (линейных) напряжений UBA, UAC, UCB замкнута (составляется в треугольник), поэтому нулевая последовательность в ней присутствовать не может. Система векторов фазных напряжений UA, UB, UC при наличии нулевой последовательности разомкнута; геометрическая сумма векторов равна утроенному значению напряжения нулевой последовательности.
Воздействие несимметричной системы напряжений на электрооборудование такое же, как трех симметричных систем. Суть этого воздействия на однофазные и трехфазные ЭП различна. Для однофазных ЭП значение имеет лишь напряжение той фазы, к которой они подключены. Так как средства РН в ЦП изменяют напряжения одинаково во всех трех фазах, то соотношение между напряжениями остается неизменным. В результате отклонение напряжения во всех фазах в ряде случаев не удается поддерживать в допустимых пределах.
Для трехфазных ЭП (например, трехфазных двигателей) воздействие обусловлено обратным чередованием фаз напряжения обратной последовательности. Так как U1 значительно больше U2 , двигатель вращается в соответствии с чередованием фаз прямой последовательности, а обратная оказывает на него тормозящее действие.

Рис. 8.2. Разложение несимметричной системы векторов на симметричные составляющие
Это вызывает некоторое снижение скорости вращения асинхронного двигателя (увеличивается скольжение s), скорость же вращения синхронного двигателя, естественно, измениться не может. В обмотках двигателей возникает ток обратной последовательности, значение которого определяется сопротивлением обратной последовательности обмоток.
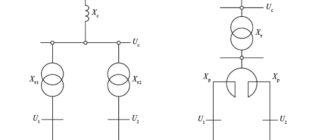
Сопротивление обмоток двигателя зависит от скольжения ротора относительно статора s и выражается зависимостью, показанной на рис. 8.3.
При нормальной работе асинхронного двигателя скольжение мало (s << l), для синхронного двигателя s = 0, поэтому сопротивление двигателя xд близко или равно xc .

Рис. 8.3. Зависимость сопротивления асинхронного двигателя от скольжения
Для заторможенного двигателя s = 1, а сопротивление резко падает до хк. Отношение xc /хк определяет кратность пускового тока (обычно kп = 4 – 7). При увеличении скольжения до s = 2 (поле статора вращается в одну сторону, а ротора – в другую, что имеет место для токов обратной последовательности) значение хд практически не изменяется по сравнению с хк. А это значит, что для токов обратной последовательности сопротивление двигателя в kп раз меньше, чем для прямой последовательности. Поэтому, например, при возникновении на вводе двигателя с kп = 7 напряжения обратной последовательности U2 = 3 % ток обратной последовательности в его обмотках составит 21 % тока прямой последовательности, что вызовет их дополнительный нагрев.
Классическая запись уравнений связи между векторами U А, U В, U С и векторами U 1 , U 2 , U 0 симметричных составляющих имеет вид:

где множители a и a2 представляют собой операторы поворота векторов на 120° и 240°.
Уравнения (8.5) записаны для векторов фазных напряжений, очередность прохождения которыми действительной оси имеет вид UA, UB, UC. Очередность прохождения действительной оси вектора xд xс xк s 1 2 ми междуфазных напряжений имеет вид UAВ , UBС , UCA. Для междуфазных напряжений в приведенных формулах заменяют величины в соответствии с приведенной их последовательностью.
Вектор, как известно, характеризуется двумя параметрами: модулем и углом его расположения на плоскости. Использование формул (8.5) для расчета симметричных составляющих предполагает измерение не только модулей напряжений, но и углов между их векторами. Это осуществляется специальными приборами, фиксирующими моменты перехода мгновенных напряжений фаз через ноль. Погрешности измерения углов добавляются к погрешности измерения модулей напряжений и ухудшают общую точность измерения. Погрешности измерения углов увеличиваются при наличии в сети высших гармоник (иногда в точке, близкой к нулю, возникают многочисленные пересечения нуля) и при резкопеременных нагрузках, приводящих к нестабильности периода основной частоты (см. п. 8.1.1). В метрологических стандартах рекомендуется при измерениях моментов перехода мгновенных напряжений фаз через ноль принимать меры по подавлению высших гармоник. Кроме того, в практике эксплуатации сетей линейные и фазные напряжения измеряют не с помощью дорогих специальных приборов, а с помощью обычных вольтметров. При этом углы расположения векторов на плоскости остаются неизвестными.
Вместе с тем данная проблема кажется искусственной. Измерения углов не являются обязательными, если все параметры симметричных составляющих, включая и углы сдвига между ними, можно определить по строгим алгебраическим формулам на основе измерения только модулей напряжений. Такие формулы приведены ниже (выводы даны в прил. 6).
Параметры напряжений прямой и обратной последовательности междуфазных напряжений определяют по формулам:

где угол ϕ2 является углом вектора U2 по отношению к вектору U1 .
В формуле (8.6) символами a2 , a4 и a22 обозначены соответственно сумма квадратов линейных напряжений, сумма четвертых степеней и сумма попарных произведений квадратов. При определении U1 в числителе подкоренного выражения (8.6) принимают знак «+», а при определении U2 – знак «–». Если знаменатель (8.7) отрицателен, то к углу ϕ2 , определенному по (8.7), надо прибавить 180°. 278 В прил. 6 приведены также другие алгебраические выражения для прямой и обратной последовательности, дающие абсолютно идентичные результаты.
Прямую и обратную последовательности в фазных напряжениях определяют исходя из соотношений: U1ф = U1 / 3 и U2ф = U2 / 3 . Угол ϕ2ф между U2ф и U1ф связан с углом между U2 и U1 соотношением ϕ2ф = ϕ2 + 60°. Параметры нулевой последовательности нельзя определить на основе измерения только фазных напряжений – необходимо использовать уже полученные для междуфазных напряжений значения U1 , U2 и ϕ2 и вычислить по ним вспомогательные величины:

Затем вычисляют величину
После этого параметры напряжения нулевой последовательности определяют по формулам:

Приведенные формулы являются точными алгебраическими выражениями, так как получены без допущений. При компьютерной обработке данных сложность формул не имеет значения, поэтому применять приближенные формулы не рекомендуется. Кроме того, симметричные составляющие приходится рассчитывать и для токов, а в них обратная и нулевая последовательности имеют гораздо более высокие значения, чем в напряжениях. Поэтому допущения, принятые при выводе приближенных формул для напряжений (например, пренебрежение заведомо малыми величинами), могут оказаться неприемлемыми при использовании этих формул для токов.
В оценочных расчетах прямую последовательность можно принимать равной среднему значению трех измеренных напряжений, а обратную – равной 62 % разности наибольшего и наименьшего значений междуфазных напряжений. В фазных напряжениях обычно U0 >> U2ф. В связи с этим величиной U2ф можно пренебречь. Тогда значение U0 можно принимать равным 62 % разности наибольшего и наименьшего фазных напряжений.
При точных расчетах необходимо иметь в виду проблему соответствия фазных и междуфазных напряжений. Три междуфазных напряжения, полученные в результате замера, всегда «складываются» в треугольник, даже если измерены с погрешностью (исключение составляет практически нереальный случай, когда сумма двух напряжений меньше третьего). Следовательно, любым полученным значениям напряжений можно поставить в соответствие физически существующую систему векторов междуфазных напряжений. В связи с неизбежными при измерениях погрешностями она будет отличаться от реальной системы, но тем не менее физически будет существовать. В то же время измеренные фазные напряжения никогда не могут составить вместе с измеренными междуфазными напряжениями физически существующую систему шести напряжений. На рис. 8.4, а приведена ситуация, когда измеренные фазные напряжения не вмещаются в систему междуфазных напряжений, а на рис. 8.4, б – когда они «не дотягиваются» друг до друга. При любой, сколь угодно малой,

Рис. 8.4. Системы несимметричных линейных и фазных векторов
погрешности измерений зона неопределенности расположения нулевой точки (выпуклый или вогнутый треугольник 0AB – 0BC – 0CA) всегда будет существовать. Так как измеряемые напряжения по существу являются случайными величинами в диапазоне погрешности измерений, а вероятность попадания случайной величины в точку тождественно равна нулю, то теоретически невозможен случай такого сочетания погрешностей измерений, чтобы вектора всех трех фазных напряжений точно сошлись в одной точке.
На рис. 8.4, в показано различие положения нулевой точки, определяемого по разным парам фазных напряжений для случая, изображенного на рис. 8.4, б. Очевидно, что вычисление симметричных составляющих для физически несуществующей системы бессмысленно, поэтому необходимо сбалансировать результаты измерений. Формулы для расчета сбалансированных напряжений приведены в прил. 6.
Связь между напряжениями в узлах, токами в линии и сопротивлениями различных последовательностей выражается формулами:

При отсутствии токов I2 и I0 напряжения в узлах определяются только режимом прямой последовательности, так как U2 = U0 = 0. При неравенстве фазных параметров даже в случае симметричной трехфазной нагрузки (I2 = 0 и I0 = 0) возникают напряжения U2 = Z21 I1 и U0 = Z01 I1 .
Равенство фазных параметров нарушается при отключении фазы линии или (хотя и в значительно меньшей степени) при отсутствии транспозиции фазных проводов на линии или удлиненных ее циклах. В табл. 8.1 приведены значения взаимных сопротивлений последовательностей для нетранспонированных линий. Напряжение обратной последовательности на приемном конце такой линии составит 8–10 % от потерь напряжения прямой последовательности. Несимметричная система напряжений возникает и на шинах потребителей, питающихся от участков, находящихся внутри полного цикла транспозиции.
Таблица 8.1
Параметры линий 110–750 кВ

* Волновое сопротивление и натуральную мощность определяют по формулам: 2 нат /; /. xb P U ρ