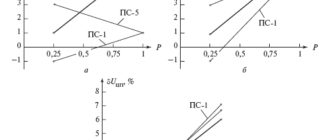
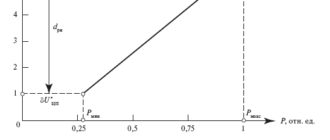
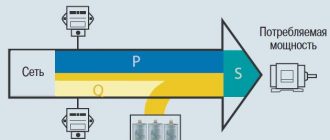
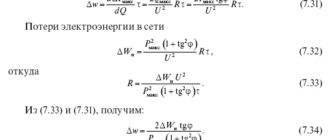Такой учет включает в себя четыре аспекта, поэтому если утверждается, что расчет проведен с учетом влияния КУ на напряжение, следует уточнить, учет каких аспектов имеется в виду.
- Первый аспект. Так как потери мощности и энергии в сети зависят от напряжений в узлах, то при их расчете до и после установки КУ при учете происходящего при этом повышении напряжения эффект от их установки будет выше, чем при расчете по номинальному напряжению, как это сделано в предыдущих разделах.
- Второй аспект. При выбранной мощности КУ напряжения в узлах должны находиться в технически допустимых пределах. Теоретически можно представить, что в некоторых узлах КУ экономически не окупаются, но их приходится ставить, чтобы поднять напряжение выше нижнего допустимого предела. Вместе с тем соотношение стоимостей КУ и электроэнергии таково, что даже при учете в расчете эффекта только от снижения потерь электроэнергии (без учета эффекта от увеличения пропускной способности сети) экономически целесообразная мощность КУ оказывается больше необходимой по техническим условиям. Поэтому обычно нет необходимости проверять соблюдение технических условий на каждом шаге итерационного процесса, достаточно проверить это в конце расчета.
- Третий аспект. Так как установка КУ приводит к увеличению напряжений в узлах и, следовательно, к дополнительному снижению потерь мощности и энергии, то при расчете производных потерь следовало бы учесть влияние Q на U (производные станут больше, а следовательно, и оптимальная мощность КУ получится несколько больше, чем определенная без учета этого влияния).
Если производную потерь мощности по Q определить с учетом влияния Q на U, получим выражение:

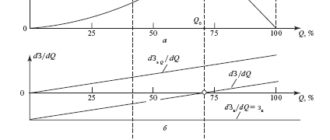
Повышение напряжения вызывает снижение потерь от передачи как реактивной, так и активной мощности, что и видно из выражения для составляющей σU . При учете влияния Q на U минимальные потери наблюдаются уже не при Q = 0, как было бы при 244 учете только первого слагаемого, а при Q, определяемом из (7.28) при приравнивании его нулю. Сокращая при этом общий множитель 2R/U 2 , получим:

где ∆Qо – потери реактивной мощности при Qо = ∆Qо .
Из уравнения (7.29) следует, что Qо = –∆Qо . Это означает, что минимальные потери в линии будут не при нулевой реактивной мощности, а при генерации в ее конце реактивной мощности, равной ее потерям в линии при нагрузке P + jQо , то есть в режиме, обеспечивающем нулевую реактивную мощность не в конце (в нагрузке), а в начале линии. Решая квадратное уравнение (7.29), получим:
Физическому решению соответствует знак «+» перед корнем.
Например, при передаче по линии 220 кВ длиной 100 км (Х = = 40 Ом) мощности P = 60 МВт по уравнению (7.30) получим Qо = = –2,9 Мвар, то есть минимальные потери в линии будут при генерации в ее конце реактивной мощности 2,9 Мвар. При учете затрат на КУ режим с перекомпенсацией, естественно, не будет оптимальным, однако определение производных с учетом влияния Q на U приведет к некоторому увеличению оптимальной мощности КУ.
В приведенном расчете мы не учли еще одно обстоятельство: в линии происходят не только потери реактивной мощности на сопротивлении Х, но и ее генерация QC . При учете только одного участка линии на потери в линии в соответствии с П-образной схемой замещения на расчете сказывается только половина этой генерации, относимая к ее конечному узлу. При расчете производных в узлах сложной сети в расчете будут участвовать полные генерации реактивной мощности всеми линиями, относимые своими половинами к узлам присоединения, за исключением половины генерации линиями, присоединенными к ЦП (балансирующему узлу).
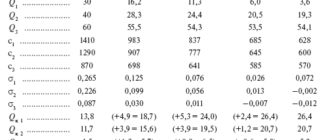
При учете емкостной генерации оптимальная мощность КУ в конце рассматриваемой одной линии не только снизится на QC /2, но и в производной (7.28) дополнительно появится отрицательное слагаемое σU c = –2QC RX/U 4 . При потреблении в конце линии 220 кВ с указанными выше параметрами реактивной мощности Q = 30 Мвар и генерации реактивной мощности, отнесенной к конечному узлу, QC = 6,5 Мвар слагаемые производной (7.28) при начальных условиях составят (без сомножителя R ∙ 10–3): σQ = 0,97; σU = 0,14; σU c = 0,0013. 245 Сопоставление этих цифр показывает, что при расчете производных в данном случае учет влияния Q на U необходим в части влияния U на потери в линии (σ = 0,97 + 0,14 = 1,11) и практически несущественен в части влияния U на емкостную генерацию.
4. Четвертый аспект. Он касается учета статических характеристик нагрузки (СХН). Под СХН понимается зависимость мощности, потребляемой нагрузкой неизменного состава, от напряжения в узле. При увеличении напряжения на вводах ЭП возрастает потребление ими и активной, и реактивной мощности. Что касается активной мощности, то увеличение ее потребления нельзя рассматривать как увеличение потерь. Электроприемник выполняет при этом большую работу, чем до повышения напряжения. Если это 2 ЭП периодического действия (например, насос), то он будет включаться на меньшее время для выполнения той же работы, потребляя ту же электроэнергию. Некоторые ЭП имеют трудно контролируемую полезность (например, вентиляторы), и часто специалисты считают нерациональным увеличение потребления ими электроэнергии (чуть меньше дуют, ну и что, зато меньше платим за электроэнергию!). При таком подходе можно рекомендовать выключить вентиляторы совсем (хоть и душно, ну и что!) – будет существенная экономия электроэнергии. Возможно, некоторые ЭП работают зря (например, двигатели на холостом ходу, которые надо бы на эти периоды отключать).
Учет СХН активной мощности при выборе КУ еще мог применяться во времена, когда частота в сетях постоянно была ниже 50 Гц из-за превышения суммарной мощностью потребителей располагаемой мощности электростанций. Он был продиктован желанием с помощью централизованного воздействия снизить бесхозяйственное (а заодно и полезное) потребление электроэнергии.
При целевой установке потреблять как можно меньше, конечно, надо работать при минимально допустимом напряжении. Однако при этом надо оценить технологический ущерб (снижение производства продукции).
Что касается реактивной мощности, то увеличение ее потребления в соответствии с СХН надо учитывать только в диапазоне ступени РН трансформатора в ЦП. Если напряжение в ЦП при установке КУ выйдет за поддерживаемое значение, то будет изменено рабочее ответвление трансформатора и напряжение опять снизится до прежнего предела (подробно эти вопросы рассмотрены в гл. 8). При этом в сети, внешней по отношению к ЦП, напряжение при установке КУ поднимется и обеспечит дополнительное снижение потерь электроэнергии.
Вывод: Резюмируя изложенное, можно сказать, что учет СХН по активной мощности необоснован, а по реактивной мощности может быть применен, но с учетом РН трансформаторами. В частности, при установке КУ в сети 0,4 кВ необходимо учитывать СХН по реактивной мощности, так как КУ изменяют напряжение на вводах ЭП в этой сети и слабо влияют на напряжение в сетях более высоких напряжений. При выборе же КУ в сетях энергоснабжающих организаций учет СХН ошибочен. После установки КУ при существенном их влиянии на напряжения в узлах рабочие ответвления трансформаторов 220–35/6–10 кВ будут изменены и потребление энергии опять вернется на прежний уровень. Поэтому при проведении расчетов по выбору КУ с помощью программ расчета УР (а они имеют возможность учитывать СХН) такой учет не должен осуществляться.