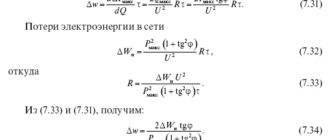Под сложной сетью в данном случае понимается сеть со многими узлами. В такой сети нельзя определить оптимальную мощность КУ в каждом узле, рассматривая его отдельно. Изменение потока реактивной мощности на каждом участке сети определяется КУ, установленными во всех ее узлах. Установка КУ в одном узле изменяет показатели эффективности их установки в других узлах. В этом случае ставится задача определения оптимального сочетания мощности и мест установки КУ, обеспечивающих минимум суммарных затрат. Такое решение должно также обеспечивать допустимые уровни напряжений в узлах. Последние обычно задаются ограничениями в форме неравенств (не ниже Uмин и не выше Uмакс ).
Для решения таких задач обычно используются градиентные методы оптимизации, реализующие итерационные алгоритмы постепенного приближения к оптимальному решению. Для определения направления движения к минимуму рассчитывают частные производные суммарных затрат (целевой функции) по мощности КУ в каждом узле. Физически они представляют собой удельные парциальные снижения суммарных затрат, руб./квар в год, при установке единичной мощности КУ в различных узлах. Далее малую мощность КУ (порцию КУ) распределяют между узлами пропорционально значениям производных.
Очевидно, что при таком распределении большая часть порции КУ попадет в узлы с большими значениями производных, так как снижение реактивной мощности в этих узлах наиболее сильно снижает суммарные затраты. При новых значениях реактивной мощности в узлах вновь определяют частные производные, которые будут иметь меньшие значения, чем на предыдущем шаге. Следующую порцию суммарной мощности КУ распределяют между узлами пропорционально новым значениям производных и т. д.
На каждом шаге оптимизации рассчитывают УР сети и проверяют соблюдение условия по допустимым уровням напряжения в узлах. В расчет вовлекаются также трансформаторы связи сетей различных классов напряжения, выбор оптимальных коэффициентов трансформации которых позволяет ввести уровни напряжения в узлах в допустимые пределы
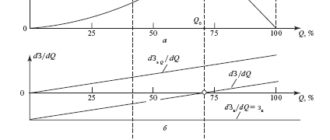
При изменившихся через несколько итераций реактивных нагрузках узлов некоторые производные могут стать отрицательными, что говорит о завышенной мощности КУ, определенной для этих узлов на предыдущих итерациях. При распределении новой порции КУ в эти узлы будет добавляться отрицательная порция мощности КУ и мощность КУ в них снизится, а в узлах с положительными значениями производных продолжит увеличиваться. Расчет заканчивается, когда производные в узлах с накопившейся мощностью КУ становятся близкими к нулю, что говорит о том, что дальнейшее увеличение или уменьшение мощности КУ приведет только к увеличению суммарных затрат (достигнута точка 0 на рис. 7.1, а для всех узлов).
Для проведения итерационных расчетов целевую функцию (7.9) выразим через передаваемую в узел реактивную мощность, произведя замену Q = Qн – Qк и исключив неиспользуемую величину Pн:

Вектор частных производных (обозначим их для простоты σ) с использованием матричных обозначений (см. прил. 4) имеет вид:

Проиллюстрируем расчет оптимальной мощности КУ на примере схемы рис. П4.2. Реактивные нагрузки узлов примем равными 30; 40 и 60 Мвар; τ = 4000 ч; bэ = 2 руб./кВт·ч (cэ = τ bэ = 8 млн руб./МВт). Удельная стоимость КУ кк = 800 руб./квар (0,8 млн руб./Мвар), ежегодные затраты на обслуживание и ремонт КУ p0 = 5 %; t ок. пр = 5 лет. При этих данных b = 2 cэ / U 2 = 2 · 8 / 2202 = 0,33 · 10–3.
Приведенные к году удельные затраты на КУ определяем по формуле (7.8):
![]()
Подставив данные в формулу (7.19), получим выражение для численного определения производных:

Вычислим значения элементов матрицы c:

Умножая значения c на 0,33 · 10–3, получим следующие значения производных:

Численные значения элементов матрицы σ означают, что при установке единицы мощности КУ в первом узле суммарные годовые затраты снижаются на 0,265 млн руб., во втором на 0,226 млн руб., в третьем на 0,087 млн руб. Задача оптимизации состоит в определении мощностей КУ в узлах, при которых все производные станут равными нулю. Сделаем первый шаг, распределив между узлами суммарную мощность КУ, равную 30 Мвар (шаг итерации). Распределяя ее пропорционально значениям производных (7.21), получим мощности КУ в узлах Qк = 13,8; 11,7 и 4,5 Мвар. Снизившиеся реактивные нагрузки узлов Q = Qн – Qк станут равными 16,2; 28,3 и 55,5 Мвар.
Полученные значения реактивных нагрузок вновь подставляют в (7.19) и определяют производные в новой точке. По мере приближения производных к нулю шаг итерации, естественно, приходится уменьшать, чтобы не проскочить нулевую точку. Как в любом итерационном процессе, чем больше делается итераций, тем ближе к нулевому значению можно привести производные.
В связи с уменьшением шага мощности КУ изменяются все в меньшей степени. Существуют алгоритмы определения оптимального значения шага на каждой итерации, основанные на анализе вторых производных целевой функции. Если первая производная показывает скорость изменения суммарных затрат при изменении мощности КУ 235 в узле, то вторая производная показывает, насколько быстро изменяется первая производная. Здесь такие алгоритмы не рассматриваются. В связи с тем, что в процессе последовательных приближений достичь точного приведения производных к нулю невозможно (можно лишь бесконечно приближаться к нему), устанавливают допустимое отличие производных от нуля, при котором процесс итераций заканчивают.
Примем это отличие равным 7,5 % удельных затрат на КУ, то есть 0,015 млн руб./Мвар в год. В данном примере шаги итерации принимались равными: на первой итерации 30 Мвар, на второй и третьей по 10 Мвар, на четвертой 3 Мвар. На пятой итерации производные стали меньше 0,015 руб./Мвар в год. Значения величин, вычисление которых подробно описано для первой итерации, приведены ниже для всех итераций:

Из приведенных результатов видно, что производная σ3 на четвертой итерации стала отрицательной. Это говорит о том, что мощность КУ в узле 3, увеличивавшаяся на предыдущих итерациях, при новой мощности КУ в остальных узлах стала излишней и была уменьшена на 0,6 Мвар. На пятой итерации производная стала отрицательной и во втором узле. Следующая итерация с шагом, например, 1 Мвар приведет к незначительному снижению мощности КУ во втором и третьем узлах и увеличению в первом узле (суммарное изменение равно шагу).
Данный пример приведен с целью иллюстрации порядка расчета. При программной реализации расчетов по выбору КУ все величины вычисляются более точными методами. В частности, потери 236 электроэнергии вычисляют не методом τ , а более точными методами 2 или 3 (см. гл. 2), на каждой итерации учитывают изменение конфигурации графиков реактивной нагрузки в узлах, влияние КУ на напряжение в узлах (его увеличение увеличивает эффективность КУ и приводит к увеличению их оптимальной мощности) и другие факторы. Значения производных в силу трудоемкости получения матрицы узловых сопротивлений обычно определяют численным методом. В каждом узле поочередно изменяют реактивную мощность на небольшую величину и рассчитывают произошедшее при этом изменение потерь мощности в сети. Частное от деления изменения потерь на изменение реактивной мощности и является производной.
Чтобы завершить пример, вычислим экономические показатели полученного решения. Потери активной мощности в сети, обусловленные передачей активной мощности, в начальных условиях составляли:

а при конечных нагрузках

Снижение потерь составило 2,1 МВт, что соответствует снижению затрат на потери 2,1 · 8 · 10–3 = 16,8 млн руб. в год. Капиталовложения на приобретение, транспортировку и монтаж КУ ККУ = = 53 · 0,8 = 42,4 млн руб. Ежегодные затраты на их обслуживание и текущий ремонт Зо = po ККУ /100 = 5 · 42,4 /100 = 2,12 млн руб., что уменьшает ежегодный эффект от капиталовложений до 16,8 – 2,12 = = 14,68 млн руб. в год.
Срок окупаемости капиталовложений в суммарную мощность КУ составляет ок 42,4 2,9 14,68 T = = года.
В связи с тем, что на практике установку КУ во всех узлах не удается осуществить одновременно, возникают вопросы об экономических показателях каждого КУ в отдельности и целесообразной последовательности установки. Формулы расчета потерь мощности содержат квадраты собственных нагрузок и произведения нагрузок различных узлов. Разделить мультипликативную функцию на аддитивные составляющие, каждая из которых зависела бы только от своего аргумента, невозможно. Поэтому снижение потерь мощности в сети и экономический эффект от установки КУ в конкретном узле можно определить лишь при фиксированных нагрузках остальных узлов. Экономический эффект от установки КУ в рассматриваемом узле будет разным в случаях установки КУ только в этом узле, когда остальные нагрузки остаются на исходных значениях, или когда нагрузки в остальных узлах принимаются на уровне, соответствующем установленным КУ в узлах.
Решение второй задачи является фактически распределением между тремя КУ суммарного эффекта. Произведение первого члена строчной матрицы Q на первый член столбцевой матрицы с в (7.22) и (7.23) характеризует вклад в потери мощности в сети реактивной нагрузки первого узла, произведения вторых членов – вклад второго узла, третьих членов – третьего узла. Для первого узла вклад в потери при начальных нагрузках составляет δPнач1 = 30 · 1410/2202 = = 0,87 МВт, а при конечных нагрузках δPкон1 = 3,6 · 628/2202 = = 0,047 МВт. Рассчитанные аналогичным образом вклады всех узлов в потери мощности в сети приведены ниже, МВт:

Формула для определения экономического эффекта от КУ в i-м узле имеет вид:

где индексами «нач» и «кон» обозначены величины, соответствующие начальным и конечным значениям реактивных нагрузок узлов.
Для первого узла
![]()
Рассчитанные таким же образом значения для второго и третьего узлов составляют Э2 = 5,77 млн руб. в год и Э3 = 3,36 млн руб. в год. Сумма эффектов равна определенному выше суммарному значению 14,68 млн руб. в год. Сроки окупаемости капиталовложений и удельные эффекты (эi = Эi /Qк i , млн руб./Мвар в год) от установки КУ в каждом узле составляют:
При ограниченных капиталовложениях может ставиться задача определения узла с наиболее быстрой «отдачей» затрат. В силу квадратичной зависимости потерь от нагрузки ее снижение на единицу 238 в зоне больших значений дает гораздо больший эффект, чем в зоне 2 малых значений. Поэтому небольшая мощность КУ использует наиболее эффективный диапазон снижения потерь, имеет хорошие удельные показатели, но небольшой суммарный эффект, так как он определяется произведением удельных показателей на мощность КУ. В нашем примере таким узлом является узел 3.
Оптимальная стратегия установки КУ в сети зависит от предполагаемого места их установки в узле (на высоком или на низком напряжении подстанции) и от оценки инвестором программы капиталовложений и получаемого эффекта. Установка КУ напряжением 35–220 кВ предполагает одноразовый монтаж всей мощности в узле, а мощность КУ напряжением 6–10 кВ может наращиваться с помощью добавляемых комплектных КУ малой единичной мощности. Поэтому для КУ 35–220 кВ рассматривается оптимальная последовательность их установки в узлах, а для КУ 6–10 кВ – стратегия их наращивания.
В первом случае наиболее целесообразно начать с установки КУ в узле 3. Во втором случае наращивание мощности в узле целесообразно начинать с узлов с наиболее высокими значениями производных. В условиях примера это узел 1 (σ1 = 0,265). Мощность КУ в этом узле следует наращивать до тех пор, пока производная в узле 1 не снизится до значения производной в узле 2. Далее надо наращивать мощность КУ одновременно в узлах 1 и 2 до тех пор, пока производные в узлах 1 и 2 не сравняются с производной в узле 3. После этого мощность наращивается одновременно во всех узлах до достижения оптимальных значений, рассчитанных выше.
Выбор оптимальной мощности КУ и стратегии их установки в сетях при всех описанных постановках задачи может быть выполнен с помощью программы «КРМ-стандарт», разработанной А. В. Артемьевым под руководством автора книги.