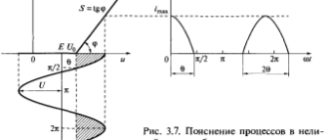
“Амплитудной модуляцией” называется изменение амплитуды несущего сигнала в соответствии с модулированным колебанием. Например, имеем высокочастотное несущее колебание (Формула) и первичный сигнал (Формула), где U0 — постоянная составляющая. Результирующий амплитудно-модулированный сигнал получим на основе перемножения несущего колебания и первичного сигнала:
![]()
Пусть x(t) является гармоническим колебанием с частотой Ω, т.е. х(t) = XcosΩt. Тогда (Формула). Здесь x(t) — медленно меняющаяся во времени функция по сравнению с высокочастотным колебанием ω0, т. е. Ω << ω0.
Введем следующее обозначение:
![]() — максимальное приращение амплитуды огибающей.
— максимальное приращение амплитуды огибающей.
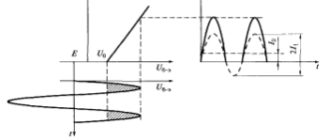
ВременнЫе диаграммы, иллюстрирующие процесс амплитудной модуляции тональным колебанием, показаны на рис. 4.1.

Рис. 4.1. ВременнЫе диаграммы, иллюстрирующие амплитудную модуляцию:
а — первичный сигнал; б — высокочастотное несущее колебание; в — модулированный сигнал
Коэффициентом модуляции называется отношение амплитуды (Формула) огибающей к амплитуде (Формула) несущего колебания, т. е. (Формула). Обычно 0 < m < 1.
Глубиной модуляции называется коэффициент модуляции, выраженный в процентах. Следовательно, можно записать
![]()
Раскроем данное выражение, что позволит определить спектр АМ-сигнала:
![]()
Из этого выражения видно, что АМ-колебание, спектр которого при модуляции одним гармоническим сигналом изображен на рис. 4.2, содержит три составляющие.
- колебание несущей частоты ω0 с амплитудой U0;
- колебания верхней боковой частоты ω0 + Ω с амплитудой (Формула);
- колебания нижней боковой частоты ω0 − Ω с (Формула).
Из сказанного можно сделать следующие выводы.
- Ширина спектра равна удвоенной частоте модуляции Δω = 2Ω.
- Амплитуда несущего колебания при модуляции не изменяется, а амплитуды колебаний боковых частот пропорциональны глубине модуляции, т.е. амплитуде модулирующего сигнала.
- При m = 1 амплитуды колебаний боковых частот равны половине амплитуды несущего колебания, т.е. (Формула). При m = 0 боковые частоты отсутствуют, что соответствует немодулированному колебанию.
На практике однотональные АМ-сигналы используются крайне редко. Более реален случай, когда низкочастотный модулированный сигнал имеет сложный спектральный состав:
![]()
Здесь частоты (Формула) образуют упорядоченную возрастающую последовательность (Формула), а амплитуды Хk и фазы φk — произвольные.
В этом случае для АМ-сигнала можно записать следующее аналитическое соотношение:

где (Формула) — парциальные коэффициенты модуляции, представляющие собой коэффициенты модуляции соответствующих компонентов первичного сигнала.

Рис. 4.2. Спектр колебаний при амплитудной модуляции одним низкочастотным гармоническим сигналом
Спектральное разложение производится так же, как и для однотонального АМ-сигнала:

Из этого разложения видно, что в спектре кроме несущего колебания содержатся группы верхних и нижних боковых колебаний. При этом спектр верхних боковых колебаний является копией спектра модулирующего сигнала, сдвинутой в область высоких частот на значение ω0, а спектр нижних боковых колебаний располагается зеркально относительно ω0.
Спектры исходного полосового сигнала и амплитудно-модулированного сигнала показаны на рис. 4.3.


Рис. 4.3. Спектры исходного полосового (а) и амплитудно-модулированного (б) сигналов
Из этой формулы видно, что, если m ≈ 1, при Ωt = 0 мощность (Формула), а при Ωt = π мощность (Формула).
Таким образом, при 100%-й модуляции, когда m = 1, мощность АМ-колебания изменяется в пределах ![]() .
.
Найдем теперь среднее значение мощности за период низкой частоты. В этом случае средняя мощность всего АМ-колебания есть сумма мощностей несущей частоты и двух боковых частот — нижней и верхней, следовательно, при сопротивлении 1 Ом нагрузки средняя мощность несущей частоты
![]()
а каждая из боковых составляющих имеет мощность
![]() Теперь несложно получить общую мощность АМ-сигнала за период колебания низкой частоты Ω:
Теперь несложно получить общую мощность АМ-сигнала за период колебания низкой частоты Ω:
![]()

Следовательно, для более эффективного использования мощности передатчика целесообразно передавать модулированный сигнал без колебания несущей частоты. Кроме того, для уменьшения ширины спектра, занимаемого сигналом, желательно передавать только одну из боковых полос, поскольку оба боковых колебания содержат одну и ту же информацию.