При обработке сигналов важно знать, какие составляющие колебания являются энергетически значимыми и какова ширина спектра колебания. Ответ на эти вопросы дают соотношения Рэлея — Парсеваля для периодических и непериодических колебаний.
Среднюю мощность периодического сигнала S(t) в соответствии с выражением (2.10) можно представить в виде
Возведя в квадрат выражения под знаком суммы, получим слагаемые вида
интегрирование произведений косинусов и синусов по свойству ортогональности функции — нуль.
Следовательно,
В математике выражение (2.19) называется равенством Рэлея—Парсеваля, из которого следует, что средняя мощность периодического колебания равна сумме средних мощностей составляющих его гармоник.
Зависимость P = f(ω) называется спектром мощности периодического колебания.
Для непериодических колебаний равенство Рэлея—Парсеваля имеет вид
Левая часть равенства (2.20) определяет энергию колебания. Следовательно, 
— есть не что иное как энергия колебания, приходящаяся на один радиан полосы частот для текущего значения ω. Иными словами, G(ω) является спектральной плотностью энергии колебания S(t) и характеризует распределение энергии в полосе частот колебания. Спектры мощности и спектральные плотности энергии называются энергетическими спектрами.
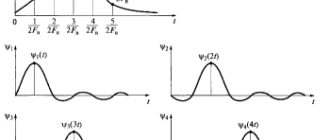
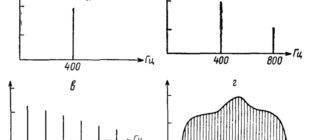
Теоретически реальные колебания как ограниченные во времени имеют бесконечный спектр. Однако рассмотрение спектров различных колебаний (например, представленных в табл. 2.1) показывает, что спектральная плотность амплитуд уменьшается (монотонно или немонотонно) с ростом частоты.
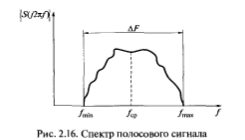
Этот же вывод следует и из анализа равенств Рэлея — Парсеваля (2.19) и (2.20), в соответствии с которыми Аk → 0 при k → ∞, а также (Формула) при ω → ∞. В противном случае ряд (2.19) был бы расходящимся (так как мощность бесконечна) или интеграл (2.20) был бы расходящимся (так как энергия бесконечна). Это позволяет условно говорить о занимаемой полосе частот, или ширине спектра колебания. Наиболее распространена так называемая энергетическая ширина спектра, определяемая как полоса частот ΔF в пределах которой сосредоточена бОльшая часть средней мощности (энергии) колебаний.
Строгих правил относительно процентного содержания мощности (энергии) в пределах занимаемой полосы частот часто не существует (обычно это 90 … 99%). Соответственно, задавая значение δ = 0,9 … 0,99, ширину полосы ΔF можно определить с использованием соотношений (2.19) или (2.20).
Так, например, для непериодических колебаний, используя выражение (2.20), можно записать
Решив это интегральное уравнение (обычно численно), можно определить ΔF.
