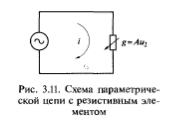
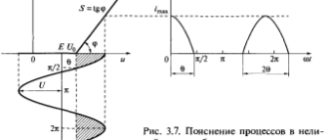
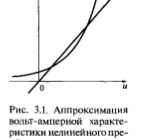
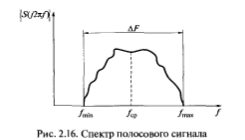
Как следует из преобразования Фурье, существует взаимосвязь между действиями, совершаемыми с сигналами во временнОй области, и их представлениями в частотной области, и наоборот. Эта взаимосвязь формулируется в виде теорем о спектрах, применение которых оказывается весьма полезным на практике.

Таблица 2.3
В табл. 2.3 представлена формальная трактовка некоторых из этих теорем. В последней строке этой таблицы приведена пара преобразований Фурье. Для каждой теоремы показаны операции с сигналом во временнОй области и даны соответствующие спектральные представления.
Приведем краткие формулировки теорем о спектрах.
- Теорема сложения спектров: спектр суммы колебаний равен сумме спектров слагаемых колебаний.
- Теорема временнОго сдвига (запаздывания): при сдвиге колебания во времени (изменении начального момента отсчета времени) спектральная плотность амплитуд сохраняется постоянной, а спектр фаз изменяется на значение, пропорциональное частоте и времени сдвига с учетом его знака.
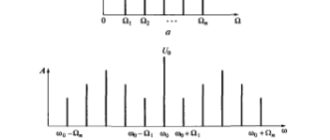
- Теорема смещения (модуляции): умножение колебания S(t) на (Формула) приводит к смещению его спектра на значение ω0.
- Теорема об изменении масштаба: растяжение колебания во времени (a > 1) влечет за собой сжатие его частотного спектра и увеличение спектральной плотности амплитуд. Сжатие колебания во времени (а < 1) приводит к расширению его частотного спектра и уменьшению спектральной плотности амплитуд.
- Теорема о свертке: свертка двух колебаний S1(t) и S2(t) соответствует перемножению их спектров.
Остальные приведенные в табл. 2.3 теоремы не требуют пояснения.